.
Factor the Polynomial completely
p(x)= x^5+6x^3+9x
~~~~~~~~~~~~~~~~~~~~
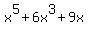 =
= 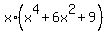 =
! Notice that x^4 + 6x^2 + 9 =
=
! Notice that x^4 + 6x^2 + 9 = 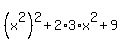 =
= 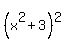 .
Therefore, you can continue this chain of equalities in this way
=
.
Therefore, you can continue this chain of equalities in this way
= 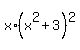 =
The only real zero is z= 0. All other zeroes are complex zeroes.
So, you can continue in the complex domain
=
=
The only real zero is z= 0. All other zeroes are complex zeroes.
So, you can continue in the complex domain
= 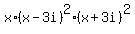 .
Now you can see that there is one real zero x= 0 of multiplicity 1,
complex zero x= 3i of multiplicity 2, and
complex zero x= -3i of multiplicity 2.
.
Now you can see that there is one real zero x= 0 of multiplicity 1,
complex zero x= 3i of multiplicity 2, and
complex zero x= -3i of multiplicity 2.