Question 1098844: Hi,
I would appreciate if someone might help here.
Exercise instructions: Express following in form X + Y*2^(1/2); X and Y are rational numbers:
(7 + 5 * 2^(1/2))^(1/3)
The answer given is: 1 + 2^(1/2)
I have no idea how they got there.
Thanks
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If we are not given the solution, we just need to solve
 . .
If you like square roots better than fractional exponents,
feel free to write 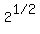 as as  . .
I will have to write  as as  in some places, in some places,
to make sure that you see the whole fractional exponent,
because I do not see the whole exponent in 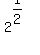 . .




Now we only need the one and only rational pair solution to
 . .
When looking for rational solutions for polynomial equations,
we just try numbers that look promising.
Substituting  in those two equations, in those two equations,
we find that they are a solution.
Knowing that there was only one real solution to be found,
we know that  gives us gives us
THE one and only answer, which is
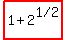 , also known as , also known as 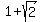 . .
NOTE: If the question was stated as "prove that  ," all we would have needed to do is calculate ," all we would have needed to do is calculate
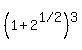 , by expanding that cube of a binomial, , by expanding that cube of a binomial,
and simplifying as needed.
As asked, the problem was not as difficult as it was intimidating,
encouraging you to give up.
|
|
|