SOLUTION: Find a polynomial of lowest degree with rational coefficients that has 3 and 4i as some of its zeros.

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Find a polynomial of lowest degree with rational coefficients that has 3 and 4i as some of its zeros.      Log On


   

Question 1098020: Find a polynomial of lowest degree with rational coefficients that has 3 and 4i as some of its zeros.
Answer by ikleyn(52778) About Me  (Show Source):
You can put this solution on YOUR website!
.
For polynomials with real coefficients, complex roots "z" always go in pairs 

(z, z-conjugated).


The conjugated to  4i  is the complex number  -4i.


So, your polynomial is  a*(x-3)*(x-4i)*(x+4i) = 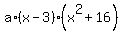a%2A%28x-3%29%2A%28x%5E2%2B16%29.


The leading coefficient "a" is an arbitrary real number, or, 
if you really are seeking for rational coefficients, then "a" must be a rational number.