SOLUTION: E is a volcano. During a recent eruption, the volcano spewed copious amounts of ash. One small piece of ash was ejected from the volcano with an initial velocity of 368 ft/sec. The

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: E is a volcano. During a recent eruption, the volcano spewed copious amounts of ash. One small piece of ash was ejected from the volcano with an initial velocity of 368 ft/sec. The      Log On


   

Question 1092831: E is a volcano. During a recent eruption, the volcano spewed copious amounts of ash. One small piece of ash was ejected from the volcano with an initial velocity of 368 ft/sec. The height H, in feet, of our ash projectile is given by the equation:
H = -16t^2 + 368t,
Where t is the time in seconds. The graph of this equation will be a parabola. We will assume that the volcano has no height. In other words, when H=0 at t=0.
Question 1. When does the ash projectile reach the its maximum height? t=?
Question 2. What is its maximum height?
Question 3. When does the ash projectile return to the ground?
Answer by ikleyn(52754) About Me  (Show Source):
You can put this solution on YOUR website!
.
Q3.  To answer question 3, solve the equation

     H(t) = 0,   or, which is the same,   -16t^2 + 368t = 0.


     It is easy: factor the left side to get  -16*t*(t - 23) = 0.


     t = 0  corresponds to the very beginning of the process, when the ash started its way up.
     The other root is t = 23 seconds, and it is exactly the time moment when the piece of ash will return to the ground.



Q1.  The plot H = H(t) is the parabola, and it reaches its maximum in the time moment exactly at midpoint between 
     the roots t= 0  and  t= 23, i.e. at the time moment t= 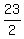23%2F2 = 11.5 seconds.



Q2.  To find the maximal height, simply substitute t= 11.5 into the quadratic function and calculate. I leave these calculations to you.


So, I answered all your questions.


---------------------------
It is one way and one method to solve the problem.

There is another way and another method.

Learn it looking into the lessons
    - Problem on a projectile moving vertically up and down
    - Problem on an arrow shot vertically upward
    - Problem on a ball thrown vertically up from the top of a tower
    - Problem on a toy rocket launched vertically up from a tall platform

Also,  you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this textbook under the topic "Projectiles launched/thrown and moving vertically up and dawn".


Save the link to this online textbook together with its description

Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson

to your archive and use it when it is needed.