Question 108815: We just started factoring polynomials,and I don't understand when you first look at a problem,if it has a greater common factor or not.I did read my book but I'm still confused.could you explain this to me,and possibly give me some examples.I appreciate all the help you all have given me.
Thanks in advance sincerely,JH
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! The first thing that you do when factoring is take out all of the 
Example:
 ………..when factor the numbers ………..when factor the numbers  , ,  , and , and
 , you will see that each one is divisible by , you will see that each one is divisible by  . .
Also, when you look at  , ,  , and , and  , you will see that , you will see that
all of them you can divide by 
So, the  here is here is  . .
Then you can write your equation like this:
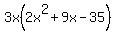
Then you factor 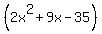 . .
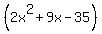 ….write ….write  as as 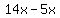
 ……..group first and third term, second and fourth term ……..group first and third term, second and fourth term
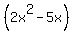 + ( + (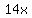 – –  )……..here, in first term common factor is )……..here, in first term common factor is
 , and in second term common factor is , and in second term common factor is 
so, we can write it:  , and , and 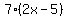 where we see that common where we see that common
factor is 
now we can write 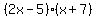
if we go back to our equation, we can write it like this:
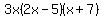
Remember:
Factoring a polynomial is the 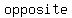 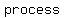 of multiplying polynomials. of multiplying polynomials.
The 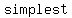 type of factoring is type of factoring is  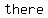 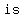 a factor a factor   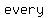 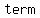 . .
Recall that the 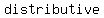 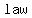 says that says that 
If you see something of the form 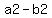 , you should remember the formula: , you should remember the formula:
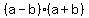 = = – – 
This only holds for a  of two squares, NOT for a of two squares, NOT for a  of two squares such as of two squares such as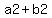 into factors with real numbers. into factors with real numbers.
Remember:
“Perfect Square Trinomial”
Recall from special products of binomials that  and and
It will help you to solve any problem. Good luck!!!!!!!!!
|
|
|