SOLUTION: 35x^4+2x^2-1=0 What is the value of x?

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: 35x^4+2x^2-1=0 What is the value of x?      Log On


   

Question 1050453: 35x^4+2x^2-1=0
What is the value of x?
Answer by ikleyn(52776) About Me  (Show Source):
You can put this solution on YOUR website!
.
35x^4+2x^2-1=0
What is the value of x?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

This equation is called biquadratic (the degrees of the unknown "x" are 4, 2 and zero).
The method of solving such equations is as follows:

Introduce new variable y = x^2.  Then your equation takes the form

35y^2 + 2y - 1 = 0.

It is just a quadratic equation, and you can apply the quadratic formula to solve it:

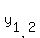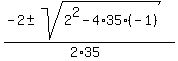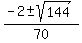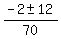y%5B1%2C2%5D = %28-2+%2B-+sqrt%282%5E2+-+4%2A35%2A%28-1%29%29%29%2F%282%2A35%29 = %28-2+%2B-+sqrt%28144%29%29%2F70 = %28-2+%2B-+12%29%2F70.

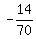y%5B1%5D = 10%2F70 = 1%2F7.  y%5B2%5D = -14%2F70 = -1%2F5.

Since y = x^2, we are interested in positive "y" only.

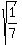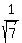Thus we have x^2 = 1%2F7 and, hence, x = +/-sqrt%281%2F7%29 = +/-1%2Fsqrt%287%29.

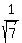Answer. The two real roots of the original equation are +/-1%2Fsqrt%287%29.

See the lesson
    - Solving polynomial equations of high degree by introducing a new variable
in this site.