SOLUTION: What is the coefficient of x^3 in this expression? (x^4 + x^3 + x^2 + x + 1)^4

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: What is the coefficient of x^3 in this expression? (x^4 + x^3 + x^2 + x + 1)^4      Log On


   

Question 1031692: What is the coefficient of x^3 in this expression?
(x^4 + x^3 + x^2 + x + 1)^4
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
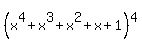
%28x%5E4+%2B+x%5E3+%2B+x%5E2+%2B+x+%2B+1%29%5E4%22%22=%22%22



The products x3*1*1*1 gives x3.  

The number of distinguishable arrangements or x3,1,1,1 is
4!/3! = 4

The products x2*x*1*1 gives x3.

The number of distinguishable arrangements or x2,x,1,1 is
4!/2! = 12

The products x*x*x*1 gives x3.

The number of distinguishable arrangements or x,x,x,1 is
4!/3! = 4

Total ways to get x3 is 4+12+4 = 20

So the coefficient of x3 is 20

Incidentally, the whole thing multiplied out is:

x16+4x15+10x14+20x13+35x12+52x11+68x10+80x9+85x8+80x7+68x6+52x5+35x4+20x3+10x2+4x+1

Edwin