Question 1020839: h(x)= 3x^4+17x^3+10x^2+x+5
The function below has at least one rational zero. Use this fact to find all zeros of the function. The function below has at least one rational zero. Use this fact to find all zeros of the function. If there is more than one zero separate them with commas. Write exact values not decimal approximations.
Thank you!!!!!!!!!!!!!! I hate math!! :-(
Found 2 solutions by richard1234, MathTherapy:
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! By the rational root theorem, the rational root is of the form

where p and q are positive integers and p is a factor of 5, q is a factor of 3. Moreover, the root must be negative (since all coefficients are positive, so it can't possibly have a positive root). So you only need to check -1/1, -1/3, -5/1, and -5/3.
Once you have found the rational root x_0, divide by (x - x_0) to obtain a 3rd degree polynomial. The 3rd degree polynomial must have a rational root; if it is rational, then you can use the rational root theorem again, otherwise you might need to use a calculator. Once you have found the second root, divide again to obtain a quadratic polynomial, in which you can solve using the quadratic formula.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! h(x)= 3x^4+17x^3+10x^2+x+5
The function below has at least one rational zero. Use this fact to find all zeros of the function. The function below has at least one rational zero. Use this fact to find all zeros of the function. If there is more than one zero separate them with commas. Write exact values not decimal approximations.
Thank you!!!!!!!!!!!!!! I hate math!! :-(
Don't hate it. Learn it, understand it, practice it and you'll love it!
Using the rational root theorem we find that there are at least 2 rational zeroes: 
This means that x = - 1, or x + 1 = 0, and x = - 5, or x + 5 = 0. FOILing the 2 factors, we get: (x + 1)(x + 5) = 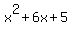
Dividing 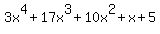 by the trinomial by the trinomial 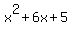 , or, , or, 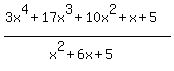 , we get: , we get: 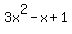
Using the quadratic equation formula to determine the other zeroes, 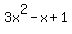 produces the complex roots: produces the complex roots: 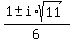 , or , or 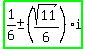
|
|
|