Question 1003702: Explain why 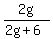 can not be simplified to 
Thanks in advance to anyone who can help! :)
Found 2 solutions by josgarithmetic, KMST:
Answer by josgarithmetic(39616)   (Show Source):
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! For  ,
 ,
so for ,  .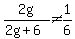
Simplifying means changing an expression to an equivalent expression,
an expression that, for every combination of values of the variables, calculates the same result,
but looks simpler to you (or to your teacher, because simplicity is in the eye of the beholder).
Simplifying does not mean magically crossing out expressions based on memorized (or maybe mis-remembered) arbitrary rules.
You cannot cross out two expressions that are the same just because both are on opposite of an equal sign or a division bar symbol.
After all,  .
You can cross out an expression that is a factor of the numerator and denominator,
as in  ,
because the crossing out really means pulling out  as a factor:
Algebra is a language, with defined symbols and "grammar" rules,
like every other language.
However, it is the easiest language I have ever seen,
with thew fewest symbols, and the fewest grammar rules.
After learning the symbols and "grammar",
the rest of algebra (and calculus) is just common sense.
However, sometimes your reasoning would not re-discover gunpowder fast enough.
In those cases, it is good to have someone show you, and for you to remember,
the clever ways that people before you (like Pythagoras and others)
used their common sense to solve problems in ways that may take you a while longer to figure out.
|
|
|
