Question 1002501: Consider the expansion of (x+y)^n.
1. How many terms does the expression contain?
2. What is the exponent of x in the first term?
3. What is the exponent of y in the first term?
4. What is the sum of the exponents in any term of the expansion ?
Show work please, thanks
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
is a formula/theorem that is usually proven in class, and then the proof is often forgotten.
1. The expression contain  terms, terms,
which is easy to see/count in the formula above,
because you see  first first 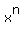 term without a term without a  , plus , plus
 terms showing terms showing  with with  different numbers as exponents, different numbers as exponents,
starting with the invisible exponent  in the term in the term  , ,
and going all the way to exponent  in the in the 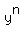 last term. last term.
2. The exponent of x in the first term is  because the term that we write first is because the term that we write first is 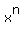 . .
There is no compelling reason to write the terms in that order,
but it is customary, and having a certain order in mind helps keep track of all those terms.
3. Since the first term is  , we can say that the exponent of y in the first term is , we can say that the exponent of y in the first term is  . .
4. The sum of the exponents in any term of the expansion is  . .
That is true for the first term,  , and is also true for all of the other terms. , and is also true for all of the other terms.
EXPLANATION OF THE FORMULA (in case you care):
The formula comes from the fact that
 with with  factors. factors.
Before simplifying, the product of those  factors would have factors would have  products made by choosing one of the variables (x or y) from each of the products made by choosing one of the variables (x or y) from each of the 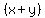 factors. factors.
Because each of those  products has products has  factors, the degree of each product (meaning the sum of the exponents of x and y) is factors, the degree of each product (meaning the sum of the exponents of x and y) is  . .
Choosing the x from each of the  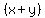 factors, we would get factors, we would get 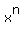 . The only one way to get the product . The only one way to get the product 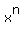 is to choose the is to choose the  term from all of the term from all of the  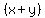 factors, factors,
so you get that product only once.
The same can be said of 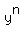 . .
Because we like to put x's before y's, and the  already had the x before the y, already had the x before the y,
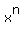 is written as the first term, and is written as the first term, and 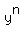 is written as the last term. is written as the last term.
We get other products multiple times
If you choose the y from one of the 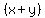 factors and the x from the others, you get products like factors and the x from the others, you get products like
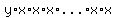 , , 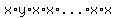 that can be written as that can be written as 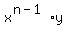 . .
Of course there are  different ways to do that, and after simplifying all those different ways to do that, and after simplifying all those  products would be accounted for in the term products would be accounted for in the term  . .
There are 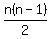 ways to choose ways to choose  y's and y's and 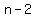 x's, x's,
and there are also 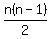 ways to choose ways to choose  x's and x's and 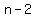 y's, y's,
and that explains the coefficients in the terms 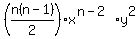 and and 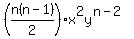 . .
|
|
|