Advanced factoring
This lesson is advanced.
It is intendent for those who want to know more.
Problem 1
Factor 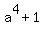 .
.
Solution
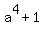 =
= 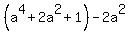 =
=  =
= 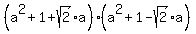 =
= 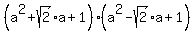 .
.
Problem 2
Factor 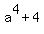 .
.
Solution
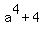 =
= 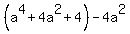 =
= 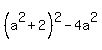 =
= 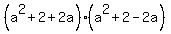 =
= 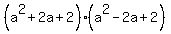 .
.
Problem 3
Prove that 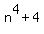 is a composed number for any natural n.
is a composed number for any natural n.
Solution
According to the solution to the Problem 2,
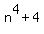 =
= 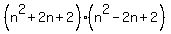 is the decomposition of the number
is the decomposition of the number 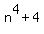 into the product of two factors
into the product of two factors  and
and 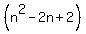 .
.
Problem 4
Factor 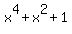 .
.
Solution
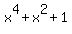 =
= 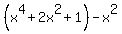 =
= 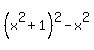 =
=  =
= 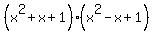 .
.
Problem 5
Factor 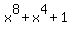 .
.
Solution
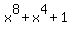 =
= 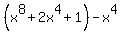 =
= 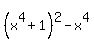 =
= 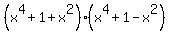 =
= 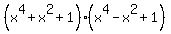 .
You can factor polynomial
.
You can factor polynomial 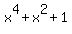 further similar to that it was done in the solution to Problem 4:
further similar to that it was done in the solution to Problem 4:
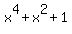 =
= 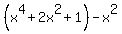 =
= 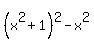 =
= 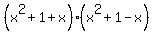 =
= 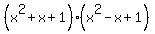 and
So,
and
So, 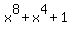 =
= 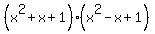 .
.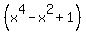 .
.
Problem 6
Factor 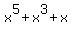 .
.
Solution
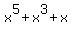 =
= 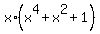 =
= 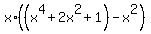 =
=  =
=  =
= 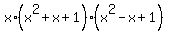 .
.
Problem 7
Factor 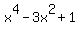 .
.
Solution
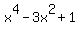 =
= 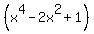 -
-  =
= 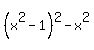 =
= 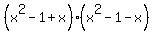 =
= 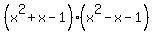 .
.
Problem 8
Given the expression x2 - kx + 81.
a) Determine the value of "k" that makes the trinomial factorable.
b) Factor it for each such value of "k".
Solution
One solution is OBVIOUS: it is k= 18.
Then x^2 -18x + 81 = (x-9)*(x-9) =  . (1)
But there is another solution, too: k= -18, which makes THIS factoring
x^2 + 18x + 81 = (x+9)*(x+9) =
. (1)
But there is another solution, too: k= -18, which makes THIS factoring
x^2 + 18x + 81 = (x+9)*(x+9) = 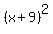 . (2)
Any student, familiar with standard binomial identities
(a+b)^2 = a^2 + 2ab + b^2, (a-b)^2 = a^2 - 2ab + b^2, (3)
should see it MOMENTARILY (!).
Even more interesting fact is that there are MANY OTHER SOLUTIONS over integer numbers.
They come from decomposition of the number 81 into the product of integer factors
81 = 1*81 = 3*27 = (-1)*(-81) = (-3)*(-27) (4)
(I just do not include the cases 81 = 9*9 = (-9)*(-9), which I considered above).
These decompositions produce the following factoring over integer numbers
81 = 1*81 --> k = 1 + 81 = 82 --> x^2 - k + 81 = x^2 - 82 + 81 = (x-1)*(x-81)
81 = 3*27 --> k = 3 + 27 = 30 --> x^2 - k + 81 = x^2 - 30 + 81 = (x-3)*(x-27)
81 = (-1)*(-81) --> k = -1 + (-81) = -82 --> x^2 - k + 81 = x^2 + 82 + 81 = (x+1)*(x+81)
81 = (-3)*(-27) --> k = -3 + (-27) = -30 --> x^2 - k + 81 = x^2 + 30 + 81 = (x+3)*(x+27)
So, over integer numbers we have 6 (six, SIX) solutions for k: 18, - 18, 82, -82, 30 and - 30, that provide
factoring of x^2 - k + 81 into the product of two binomials.
. (2)
Any student, familiar with standard binomial identities
(a+b)^2 = a^2 + 2ab + b^2, (a-b)^2 = a^2 - 2ab + b^2, (3)
should see it MOMENTARILY (!).
Even more interesting fact is that there are MANY OTHER SOLUTIONS over integer numbers.
They come from decomposition of the number 81 into the product of integer factors
81 = 1*81 = 3*27 = (-1)*(-81) = (-3)*(-27) (4)
(I just do not include the cases 81 = 9*9 = (-9)*(-9), which I considered above).
These decompositions produce the following factoring over integer numbers
81 = 1*81 --> k = 1 + 81 = 82 --> x^2 - k + 81 = x^2 - 82 + 81 = (x-1)*(x-81)
81 = 3*27 --> k = 3 + 27 = 30 --> x^2 - k + 81 = x^2 - 30 + 81 = (x-3)*(x-27)
81 = (-1)*(-81) --> k = -1 + (-81) = -82 --> x^2 - k + 81 = x^2 + 82 + 81 = (x+1)*(x+81)
81 = (-3)*(-27) --> k = -3 + (-27) = -30 --> x^2 - k + 81 = x^2 + 30 + 81 = (x+3)*(x+27)
So, over integer numbers we have 6 (six, SIX) solutions for k: 18, - 18, 82, -82, 30 and - 30, that provide
factoring of x^2 - k + 81 into the product of two binomials.
My other closely related lessons in this site are
- Solving polynomial equations of high degree by factoring
- Solving polynomial equations of high degree by introducing a new variable
- Upper_level_miracle_factoring
- Solving palindromic equations of the degree 4
- OVERVIEW of lessons on solving polynomial equations of high degree
in this site.
Use this file/link ALGEBRA-I - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-I.

