Question 947878: The difference between exterior angles of a "n" sided regular polygon and "n+1" sided regular polygon is 12 degrees. Find value of "n"
Regards
Vidhu
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The sum of the measures of the exterior angles of a convex polygon is always  . .
(The exterior angles are the angles of change of direction you must make at each corner (vertex) as you go around along the perimeter of the polygon, so of course
a whole turn around the polygon will shift your direction by  to end in the same direction you started). to end in the same direction you started).
In a regular polygon with  sides there are sides there are  congruent exterior angles, all with the same measure: congruent exterior angles, all with the same measure: 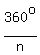 . .
Similarly, the measure of each exterior angle of an  sided polygon is sided polygon is 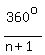 , ,
which is smaller than 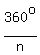 by by
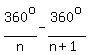 . .
For this problem,


Dividing both sides of the equal sign by 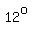 we get we get




Multiplying both sides of the equal sign times 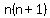 we get we get

We can say that the above equation is a quadratic equation,
and we know that a quadratic equation can have at most two solutions.
We could go through all kinds of algebra efforts to solve that equation,
but we all know that  and that and that  , ,
so we know that the two solutions are  and and  . .
(We also know that  must be an integer greater than must be an integer greater than  , ,
because a polygon must have  or more sides, or more sides,
so  makes no sense). makes no sense).
|
|
|