Question 928071: the sum of the interior angles of a regular polygon is 540 and side is 5cm .determine the following .
no.of sides
no.of diagonals
no.of triangles
central angle
interior angle
perimeter
area
apotheim
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! The sum of the measures of the interior angles of a convex polygon with  sides is
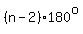
In this case,
 --> --> --> --> .
So this regular polygon has  sides. It is a pentagon.
Five sides means  vertices.
Form each vertex you can draw diagonals to other vertices.
There are  other vertices, but the  lines connecting to the next vertices to either side are not diagonals, but sides of the polygon.
So, from each vertex, you can draw  diagonals connecting to other vertices.
That would add up to  diagonals, but we would be counting each diagonal twice, for example once as a line from vertex A to vertex C, and once more as a line from vertex C to vertex A.
So there are just possible diagonals .
The diagonals from each vertex split the pentagon into  isosceles triangles with a side of the pentagon as a base, and with a diagonal of the pentagon as a base, for a total of  large triangles.
We can also figure out that there are  different large triangles, because there are  different sets of 3 vertices that can be made from the 6 vertices of the pentagon.
The diagonal also form more, smaller triangles with one or two vertices at the intersections of diagonals inside the pentagon.
Connecting the vertices of the regular pentagon to its center we form congruent triangles with angles at the center of the pentagon called "central angles".
Each central angle measures 
The measure of each of the interior angles of the pentagon is
 .
The perimeter of the pentagon is  .
The area of the regular pentagon can be calculated as the sum of the areas of the isosceles triangles formed by the lines connecting the vertices to the center.
For each of those isosceles triangles, we can take the side of the pentagon as the base, and the line connecting the midpoint of that base to the center of the pentagon as the altitude. The measure of that altitude is the height of the triangle, and the apothem of the regular pentagon.
In general, the area of the regular polygon with sides is 
  (rounded), and   .
|
|
|
