Question 782796: find the number of sides in a polygon when each interior angle is 18 degree
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! EITHER
there is a typo,
OR
there is no solution.
If all the  angles of a polygon measure angles of a polygon measure  , the polygon has , the polygon has   . .
The  angles of a polygon, are the angles between adjacent sides angles of a polygon, are the angles between adjacent sides  the polygon. the polygon.
The  angles of a polygon, are the angles between adjacent sides angles of a polygon, are the angles between adjacent sides  the polygon. the polygon.
For example, in the polygon below,
all the exterior angles measure 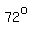 , and , and
all the interior angles measure 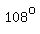 . .
(For any polygon, the measure of an interior angle and the measure of the adjacent exterior angle add up to  , because they are supplementary angles). , because they are supplementary angles).

Each exterior angle is the angle that you deviate from your previous direction as you "turn the corner around a vertex. If you go one full turn around the whole polygon, the sum of all the (exterior) angles you turn is  . .
IF all the exterior angles have the same measure, all the interior angles have the same measure (and vice versa).
IN THAT CASE, the measure of all those angles depends on the number of sides of the polygon. The measure of one exterior angle times the number of sides is the sum of all the exterior angles and equals  . .
If  = number of sides and = number of sides and  is the measure each exterior angle, then is the measure each exterior angle, then
 <--> <-->  . .
{Also,  <--> <-->  ). ).
The polygon with the least sides, would have 3 sides, with exterior angles measuring  and interior angles measuring and interior angles measuring  . With more sides the exterior angles would be smaller and the interior angles would be larger. The exterior angles could measure . With more sides the exterior angles would be smaller and the interior angles would be larger. The exterior angles could measure  and less, but the inerior angles cannot measure less than and less, but the inerior angles cannot measure less than  . .
|
|
|