Question 727836: regular hexagon ABCDEF with diagonal AC and exterior angle 1
Prove: m<2+m<3=m<1
**Note <2 is located at
I would place greater value on understanding the method rather than just the answer. Please help
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website!  Hopefully exterior angle 1 is GCB. If side CD was extended in the other direction, I had to do more drawing, but the idea is the same.
The exterior angles of a polygon are the changes in direction as you move around along the perimeter. Going counterclockwise, you go from D to C, and change direction so that instead of continuing straight towards G, you head to B. The angle GCB is an exterior angle.
If you go around clockwise, you change direction at B, and instead of heading towards G, to go towards C. Angle GBC is an exterior angle too.
You can draw 2 exterior angles at each vertex.
Because a regular polygon is symmetrical, in an regular polygon all the exterior angles are congruent. That is why it does not matter which of the exterior angles was labeled as angle 1. They all have the same measure as GCB and GBC.
Angle GBC in supplementary to angle ABC, so
In triangle ABC, with BAC=2 and BCA=3,
 
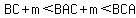
The 2 equations together result in
   -->  
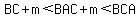And since all exterior angles have the same measure,
   
|
|
|
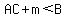
