the polygon has 12 sides, so the sum of the interior angles of the polygon is equal to (12-2)*180 = 10*180 = 1800 degrees.
there are 12 angles in the polygon and it is assumed to be a regular polygon (equal angles and equal sides), so each interior angles will be equal to 1800 / 12 = 150 degrees.
an interior angle and a vertex go together.
each vertex contains an interior angle that is formed by the sides connecting to that vertex.
the derivation of that is as follows:
a straight angle is an angle of 180 degrees.
the formula stated above of (n-2) * 180 could be re-worded to say (n-2) * a straight angle.
the formula depends on the fact that the sum of the angles of a triangle is equal to 180 degrees.
accept that and you can then derive the formula from that.
look at the picture below and then read the comments below it.
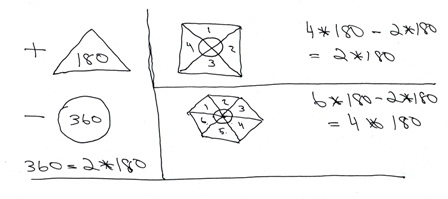
the sum of the angles in a triangle is equal to 180 degrees.
each polygon can be divided into the same number of triangles as the sum of the sides of the triangle.
each of these triangles has a vertex at the center of the polygon.
a rectangle has 4 sides and can be divided into 4 triangles.
a hexagon has 6 sides and can be divided into 6 triangle.
the sum of the angles of the triangle within the polygon is therefore equal to the number of sides * 180.
if we want to get the sum of the interior angles of the polygon, we have to subtract the sum of the central angles of the polygon.
the sum of the central angles of the polygon will always be equal to 360 degrees because the number of degrees in a circle is equal to 360 degrees.
we therefore have to subtract 360 from the sum of the angles of the triangles that form the polygon to get the sum of the interior angles of the polygon.
this means that our formula becomes:
n * 180 - 360.
now, 360 is equal to 2 * 180, so our formula becomes:
n * 180 - 2 * 180.
if we factor out the 180, then we are left with (n-2) * 180.
that's how the formula is derived.
when you have a dodecagon, then it has 12 sides.
the formula then becomes:
(12 - 2) * 180 which becomes 10 * 180.
here's a link that names the polygons.
http://mathcentral.uregina.ca/qq/database/QQ.09.96/rosa1.html
the names are usually derived from the greek names for the number of sides.