Question 394890: "How can I determine the range of possible values of the fourth side of a quadrilateral if there are three values of sides that are given? thanks!
Found 2 solutions by MathLover1, richard1234:
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website! To determine the range of possible values of the fourth side of a quadrilateral if there are
three values of sides that are given, you need to analyze carefully what kind of sides is given (are they all same length, are 2 of them same length or all have different length, what possible angles they make)
Quadrilateral just means "four sides" , and these are: a square, rhombus, rectangle, parallelogram, trapezoid and kite.
properties
* Four sides (or edges)
* Four vertices (or corners).
* The interior angles add up to 360 degrees
if  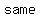  : that could be square or a rhombus (both have four-sided shape where all sides have equal length and also opposite sides are parallel and opposite angles are equal)
if  of them  :
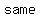-a rectangle ( it is a four-sided shape where every angle is a right angle 90° )
- a parallelogram (opposite sides are parallel and equal in length, and opposite angles are equal (angles are the same)
-an Isosceles trapezoid ( if the sides that aren't parallel are equal in length and both angles coming from a parallel side are equal)
-a kite (it has two pairs of sides, each pair is made up of adjacent sides that are equal in length)
if all have different length and one pair of opposite sides parallel it could be:
a trapezoid (has one pair of opposite sides parallel)
Answer by richard1234(7193)  (Show Source):
You can put this solution on YOUR website! Use the fact that the sum of any three sides of a quadrilateral is greater than the length of the fourth side (similar to the triangle inequality).
|
|
|
