Question 1209520: (39) Square SQUR has sides of length x. If triangle SQE is equilateral, find the area of triangle QAU.
Link to diagram: https://ibb.co/C58rZ09R
Found 4 solutions by CPhill, ikleyn, greenestamps, Edwin McCravy:
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website! Here's how to find the area of triangle QAU:
**1. Visualize the problem:**
It's helpful to draw a diagram. You have a square SQUR with side length *x*. Triangle SQE is equilateral, meaning all its sides are also of length *x*. Point A is likely somewhere related to the geometry of the square and triangle. We need more information about the location of point A to solve the problem. Let's assume A is the intersection of lines RE and QU.
**2. Find the coordinates of the points (assuming a coordinate system):**
Let's place the square in a coordinate system. Put S at the origin (0,0), Q at (x,0), U at (x,x), and R at (0,x).
Since SQE is equilateral, point E will be at (x/2, (x√3)/2).
**3. Find the equations of lines RE and QU:**
* **Line RE:** We have points R(0,x) and E(x/2, (x√3)/2). The slope of RE is:
m_RE = [(x√3)/2 - x] / [x/2 - 0] = (√3 - 2)x / x = √3 - 2
The equation of line RE (using point-slope form) is:
y - x = (√3 - 2)(x - 0)
y = (√3 - 2)x + x
y = (√3 - 1)x
* **Line QU:** We have points Q(x,0) and U(x,x). The slope of QU is undefined since it is a vertical line. The equation of the line is x=x.
**4. Find the coordinates of point A (the intersection of RE and QU):**
Since QU is the vertical line x = x, the x-coordinate of point A is *x*. Substitute *x* for x in the equation of line RE to find the y-coordinate:
y = (√3 - 1)x
So, point A is at (x, (√3 - 1)x).
**5. Find the area of triangle QAU:**
The base of triangle QAU is QU, which has length *x*. The height of the triangle is the perpendicular distance from A to the line QU. Since QU is a vertical line, the height is the horizontal distance from x to x, which is 0. The height of the triangle is the difference in the y-coordinates of A and Q. Thus the height is (√3 - 1)x - 0 = (√3 - 1)x.
Area of triangle QAU = (1/2) * base * height
Area = (1/2) * x * (√3 - 1)x
Area = (x²(√3 - 1))/2
Therefore, the area of triangle QAU is (x²(√3 - 1))/2.
Answer by ikleyn(52775)  (Show Source):
You can put this solution on YOUR website! .
Square SQUR has sides of length x. If triangle SQE is equilateral, find the area of triangle QAU.
Link to diagram: https://ibb.co/C58rZ09R
~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by @CPhill is INCORRECT.
I came to bring a correct solution.
I will use coordinate plane (x,y). To avoid missing coordinate x with the side length of the square,
I will use 'a' for the square side length.
Let's place the origin of the coordinate system (x,y) at point S.
The line EQ has an equation
y = 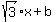 (1)
since its slope is, obviously,  . To find 'b' in this equation, substitute coordinates of
the vertex Q = {a,0) of the square into this equation
0 =  .
It gives b = 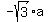 . So, equation of the line EQ is
y = 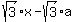 =  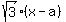. (2)
We want to find the point A as the intersection of the line SU and the line EQ.
The line SU has the equation y = -x; so, we substitute y = -x into equation (2). It gives
-x =  ,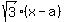
or
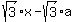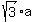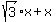-x =  ,
 =  ,
x =  .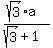
Thus we know now the x-coordinate of the point A.
So, now we can find the height h of the triangle QAU as the difference a-x:
h = a-x = a - =  =  .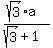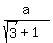
You can rationalize the denominator
h =  =  =  .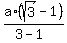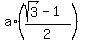
Now the area of the triangle QAU is half the product of its base 'a' by its height h =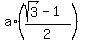
The ANSWER is : the area of the triangle QAU is
 =  =  .
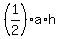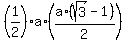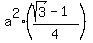Solved.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Regarding the post by @CPhill . . .
Keep in mind that @CPhill is a pseudonym for the Google artificial intelligence.
The artificial intelligence is like a baby now. It is in the experimental stage
of development and can make mistakes and produce nonsense without any embarrassment.
It has no feeling of shame - it is shameless.
This time, again, it made an error.
Although the @CPhill' solution are copy-paste Google AI solutions, there is one essential difference.
Every time, Google AI makes a note at the end of its solutions that Google AI is experimental
and can make errors/mistakes.
All @CPhill' solutions are copy-paste of Google AI solutions, with one difference:
@PChill never makes this notice and never says that his solutions are copy-past that of Google.
So, he NEVER SAYS TRUTH.
Every time, @CPhill embarrassed to tell the truth.
But I am not embarrassing to tell the truth, as it is my duty at this forum.
And the last my comment.
When you obtain such posts from @CPhill, remember, that NOBODY is responsible for their correctness,
until the specialists and experts will check and confirm their correctness.
Without it, their reliability is ZERO and their creadability is ZERO, too.
Answer by greenestamps(13198)  (Show Source):
Answer by Edwin McCravy(20054)  (Show Source):
|
|
|
