SOLUTION: Two runners start at vertices A and B simultaneously and run clockwise around the perimeter of square ABCD at the same speed. A drone flies so that it is always at the midpoint of

It is clear that without loss generality, we may think that the square side length is 1 unit.


Imagine that the square ABCD is placed in a coordinate plane such that 
point A is at the origin (0,0) and point B is (1,0).


Let first runner starts from A; second runner starts from B.


Let first runner is now on his way from A to B  x units from A.

Then second runner is on his way from B to C x units from B vertically.


The distance between them is now  

    d(x) = (1-x)^2 + x^2 = 1 - 2x + x^ + x^ = 1 - 2x + 2x^2.


So, the distance between them is this quadratic function d(x).

It has positive leading coefficient 2 at x^2 - so this parabola is opened upward and has a minimum.


The minimum is at 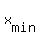  = =  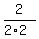= 1/2,

when both runners are in the mid of their sides.


Then the distance between them is, OBVIOUSLY, half the diagonal of the square.



If the minimum of this quadratic function is at mid-point of the side x= 1/2  (the position of the vertex),

then it is OBVIOUS that the maximum distance, d(x), will be at vertices x= 0  and/or  x= 1.



The situation will repeats from side to side; so, it is enough to consider the movement 
of runners along AB (for first runner) and along BC (for second runner).


ANSWER.  The minimum distance is when the runners are at midpoints of adjacent sides; 
         the minimum value of the distance is half of the diagonal of the square.

         The maximum distance is when the runners are in vertices of the square,
         along one common side.
         The maximum distance is the length of the square side.