Question 1209330: Given regular heptagon ABCDEFG, a circle can be drawn that is tangent to DC at C and to EF at F. What is radius of the circle if the side length of the heptagon is 1?
Found 5 solutions by ElectricPavlov, ikleyn, greenestamps, math_tutor2020, Edwin McCravy:
Answer by ElectricPavlov(122)   (Show Source):
You can put this solution on YOUR website! Certainly, let's find the radius of the circle.
**1. Find the interior angle of the heptagon:**
* The interior angle of a regular heptagon is given by:
* (n - 2) * 180° / n
* where n is the number of sides (n = 7)
* Interior angle = (7 - 2) * 180° / 7 = 900° / 7 ≈ 128.57°
**2. Find the angle at the center of the heptagon:**
* The central angle of a regular heptagon is given by:
* 360° / n
* Central angle = 360° / 7 ≈ 51.43°
**3. Find the angle ∠DCF:**
* ∠DCF = 2 * (Interior angle) - 360°
* ∠DCF = 2 * 128.57° - 360° = 257.14° - 360° = -102.86°
* Since we're dealing with angles on a circle, we can consider ∠DCF = 360° - 102.86° = 257.14°
**4. Find the angle ∠CDF:**
* ∠CDF = 180° - Interior angle = 180° - 128.57° = 51.43°
**5. Construct the circle:**
* Draw the circle tangent to DC at C and EF at F.
* Let O be the center of the circle.
* Let R be the radius of the circle.
**6. Find the distance OC:**
* In triangle ODC, ∠OCD = 90° (tangent to the circle)
* OC = R (radius of the circle)
**7. Find the distance OF:**
* In triangle OEF, ∠OFE = 90° (tangent to the circle)
* OF = R (radius of the circle)
**8. Find the distance CF:**
* CF = side length of the heptagon = 1
**9. Use the Law of Cosines in triangle OCF:**
* CF² = OC² + OF² - 2 * OC * OF * cos(∠DCF)
* 1² = R² + R² - 2 * R * R * cos(257.14°)
* 1 = 2R² - 2R² * cos(257.14°)
* 1 = 2R² * (1 - cos(257.14°))
* R² = 1 / [2 * (1 - cos(257.14°))]
* R = √[1 / [2 * (1 - cos(257.14°))]]
* R ≈ 0.4339
**Therefore, the radius of the circle is approximately 0.4339.**
**Note:**
* This calculation assumes that the circle is externally tangent to both DC and EF.
* If the circle is internally tangent to one of the sides, the calculation would be different.
Answer by ikleyn(52777)  (Show Source):
Answer by greenestamps(13198)  (Show Source):
You can put this solution on YOUR website!
The AI-produced "solution" to the problem is incorrect.
If you try to follow it, you will see that it says segment CF is a side of the heptagon, which it is not.
You should also recognize that, with the side length of the heptagon being 1, it is absurd that the answer would be that the radius of the circle tangent to DC at C and to EF at F is less than 1/2....
Following is a correct solution to the problem. In that solution, I only outline the calculations, and I only show numbers to a few decimal places. In order to learn anything from the problem, the student should go through the detailed calculations himself (I used a TI-84 calculator), and he should not do any rounding until the final answer.
Let O be the center of the circle. Then, according to the given information, OC is a radius of the circle and is perpendicular to CD, and OF is a radius of the circle perpendicular to FE.
Each exterior angle of the heptagon has a measure of 360/7 degrees, so each interior angle has a measure of 180 - (360/7) = 900/7 degrees.
Use the law of cosines in triangle DEF with DE=EF=1 and angle E having a measure of 900/7 degrees to find that the length of DF is about 1.8018.
In isosceles triangle DEF, angle DEF has measure 900/7 degrees, so each of the other two angles has measure (1/2) of (180 - (900/7)) = 180/7 degrees. That makes the measure of angle CDF 900/7 - 180/7 = 720/7 degrees.
Use the law of cosines in triangle CDF, knowing the lengths of CD and DF and the measure of angle CDF, to find that the length of CF is about 2.24698.
In pentagon OCDEF, use the known measures of angles OCD, CDE, DEF, and EFO to determine that the measure of angle COF is 720/7 degrees. Then use the law of cosines in triangle OCF, with OC and OF being radii of the circle, to find that the radius of the circle is about 1.437.
ANSWER (approximately): 1.437
Answer by math_tutor2020(3816) (Show Source):
You can put this solution on YOUR website!
I'll discuss a method of how to verify the answers that tutors ikleyn and greenestamps got.
I'm using GeoGebra to verify.
You can use the web version or you can download it to your computer.
Open up a new workbook.
Select the "regular polygon" tool.
Click anywhere on the xy grid to form the first point.
Then one unit to the right of that location is the next point.
Let's say for example the two points are at A(1,1) and B(2,1)
AB is 1 unit long.
Once A and B are in place, a dialog prompt will ask how many vertices you want. Type in 7.
This generates regular heptagon ABCDEFG where each side is 1 unit long.
Select the line tool to form lines CD and EF.
Use the perpendicular line tool to form lines HC and HF, where H is the intersection of these new perpendicular lines.
H is also the center of the circle we're after.
This circle is tangent to segment CD at point C; and tangent to segment EF at F.
The last step is to use the radius command to have GeoGebra tell us the radius of the circle.
This is approximately 1.4369973927
This value will slightly vary depending how you rounded your intermediate scratch work.
Here's the GeoGebra workbook that I used to verify
https://www.geogebra.org/calculator/xrdjx482
Let me know if you have a question about a particular construction step.
Answer by Edwin McCravy(20054)  (Show Source):
You can put this solution on YOUR website!
Since no one has drawn the figure, and also has not given an exact value
for the radius, I thought I would do so, with an exact solution in terms
of trigonometric values.
We draw perpendiculars to DC at C and to EF at F, and they must intersect
at the center of the circle. We also draw FC to make an isosceles trapezoid
from which we can get the measurements for the angles, in particular angle CFE,
which turns out to be 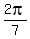 radians.
The sum of the interior angles of a polygon with n-sides =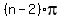 
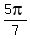So each interior angle of the regular heptagon is  , so angles E and D are  each.
Isosceles trapezoid FEDC has sum of interior angles  so angles EFC and
FCD are each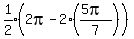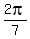  
Next we'll draw in 3 perpendiculars to FC, namely EH, DJ, and OI.
Notice that angles EFH and FOI have equal measures because they are both
complements of the same angle IFO. Therefore angle FOI also measures .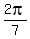
Since each side of the heptagon is 1,
(a) the hypotenuse EF of right triangle EFH is 1 and 
(b)  because HJ=ED=1 and HI is 1/2 of HJ
(c) 
So from right triangle FIO, we can now find the desired radius FO
 and 
So the exact answer for the radius is
 which can also be written as
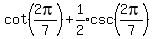 <--EXACT SOLUTION!
That's approximately 1.436997393, which approximately agrees with Ikleyn's,
and is even closer to Greenestamps', approximate solution.
Edwin
|
|
|
