SOLUTION: what is the largest diameter circle that will fit inside a regular pentagon with 2-inch sides

Algebra ->  Polygons -> SOLUTION: what is the largest diameter circle that will fit inside a regular pentagon with 2-inch sides       Log On


   

Question 1208232: what is the largest diameter circle that will fit inside a regular pentagon with 2-inch sides
Answer by ikleyn(52776) About Me  (Show Source):
You can put this solution on YOUR website!
.
what is the highlight%28cross%28largest%29%29 diameter of the circle that will fit inside a regular pentagon with 2-inch sides
~~~~~~~~~~~~~~~~~~~~~~~~


    I crossed above,  since there is  NO  the largest diameter.
    All diameters of a circle have the same length. 


Consider one of 5 isosceles triangles that make this pentagon.


The base of this triangle is 2 inches, hence, half of the base is 1 inch long.


The angle of the triangle, opposite to the base, is  360/5 = 72 degrees;
half of this angle is 36 degrees.


Let r be the radius of the circle, inscribed in this pentagon (in inches).


Then 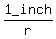 1_inch%2Fr = tan(36).


Hence,  r = 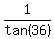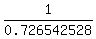1%2Ftan%2836%29 = 1%2F0.726542528 = 1.3763819 inches.


For tan(36), there is special formula  tan(36) = 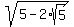sqrt%285-2%2Asqrt%285%29%29.


For deriving this formula, see, for example, this source

    https://www.cuemath.com/trigonometry/tan-36-degrees/

or many others (it is a classic in Trigonometry).



So, the answer to your question for the diameter is  

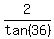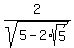    D = 2%2Ftan%2836%29 = 2%2Fsqrt%285-2%2Asqrt%285%29%29 =  2.752763841 inches.

Solved.