SOLUTION: A rhombus has an area of 200 cm^2 and one of its interior angles is 110 degrees a. Find the length of the sides b. Find the length of the longer diagonal c. Find the altitude of

Each rhombus has all its 4 sides of the same length.

Let x be the length of a side of this rhombus.

For any parallelogram, including rhombi, the area is half the product of the adjacent sides
by the sine of angle between them.


So, for the area of our rhombus, we have this equation

    x*x*sin(110°) = 200,

or

    x^2*sin(110°) = 200.


Hence,  x = 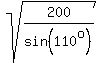 =  = 14.5889 cm, approximately.


So, question (a) is answered.


To answer question (b), use the cosine law.  Notice that the angle of the rhombus opposite to its longest
diagonal, is  110° (given).


So, the length of the longer diagonal is

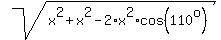     =  = 23.90105 cm, approximately.


Thus, question (b) is answered.



The altitude of the rhombus is its area 200 cm^2 divided by the side 

    the altitude = 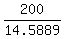 = 13.70905277  cm  (approximately).