SOLUTION: The diagonals of a parallelogram measure 16 cm and 24 cm. The shorter side measures 10 cm. 1. Find the area of the parallelogram. 2. Find the measure of the longer side. 3. Find

Diagonals of a parallelogram bisect each other.
They divide a parallelogram in 4 (four) small triangles.
The angles between the diagonals are vertical and supplementary.
So, if    is an acute angle between the diagonals, 
then the other, supplementary angle    is  .


Let's find an acute angle    between the diagonals for the given parallelogram.
Obviously, this angle is opposite to the shorter side of the parallelogram.
The halves of diagonals are 16/2 = 8 cm  and  24/2 = 12 cm long, and acute angle    
is a concluded angle between the halves of diagonals.


Write the cosine law for such a triangle

    10^2 =  +  - .


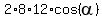It gives

     =  =  = .


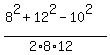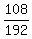These four small triangles of the subdivision have a remarkable property:
their areas are all the same.


It is easy to prove:  the area of each such a triangle is half the product of the sides
that are halves of diagonals, by the sine of the angle between them.

    area = 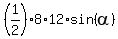  for the acute angle between diagonals

and  

    area = 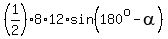  for the obtuse angle between diagonals.


But the acute angle and the obtuse angle are SUPPLEMENTARY, so, they have the same value of sine.


GREAT !


Let's calculate the sine of an angle  between the diagonals.


For the acute angle, it is  

     =  =  =  =  = .


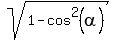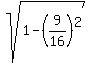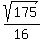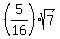For the obtuse angle,  the sine value is the same,  .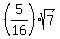


So, each of the four small triangle of the subdivision has the area

     =  = .


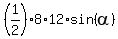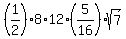The area of the whole parallelogram is then four times the area of each separate small triangle 
of the subdivision.

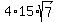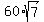So, the area of the parallelogram is   = ,  or about  158.7450787 cm^2.



To find the measure of the longer side, apply the cosine law again.
Use the obtuse-angled triangle of the subdivision.
Its sides are 8 cm and 12 cm;  the cosine of the obtuse concluded angle  = 
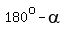is  = .


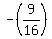So, we write for the square of the longer side of the parallelogram

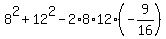
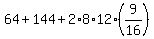      = 64+144+108 = 316.


Thus the longer side of the parallelogram is 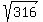  = 17.77638883 cm (approximately).



The last question is to find the smaller angle of the parallelogram,  .

Let's find it, using the shorter side of 10 cm and what we just learned about this parallelogram: 
its area is 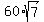   and its longer side is  .


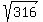The area of any parallelogram is the product of any two adjacent sides by the sine of the concluded angle.


So, for 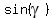  we can write this equation

    } = .


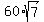Thus 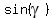  = 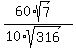 =  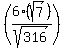= 0.893010837.


Hence,   = arcsin(0.893010837) = 63.2540602 degrees.


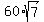ANSWER.  The area of the parallelogram is  ,  or about  158.7450787 cm^2.

         The measure of the longer side is 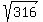 ,  or  17.77638883 cm (approximately).

         The measure of the smaller angle of the parallelogram is  arcsin(0.893010837),  or about 63.2540602 degrees.