SOLUTION: A polygon has two interior angles of 120° each and others are each 150°. Calculate The number of the polygon. The sum the interior angles

Let the number of sides be " n " (same as the number of vertices).


Then we have for the sum of the interior angles 2*120° + (n-2)*150°.


From the other side, for each n-gon, the sum of its interior angles is (n-2)*180°.


Thus we have this equation

    2*120° + (n-2)*150° = (n-2)*180°.


Simplify it step by step and find n

    2*120 = (n-2)*180 - (n-2)*150

    240   = (n-2)*(180-150)

    240   = (n-2)*30

    n-2 = 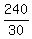 = 8

    n                  = 8 + 2 = 10.


ANSWER.  n = 10.  The polygon is a decagon (10 sides and 10 vertices).