Question 1132017: Find the Area and Perimeter for the coordinates below:
K(-2,3) L(-4,1) M(-3,-3) N(3,-3) J(4,2)
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the Area and Perimeter for the coordinates below:
 ( ( , , ) )
 ( ( , , ) )
 ( ( , , ) )
 ( ( , , ) )
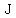 ( ( , , ) )
first sketch it:

to find perimeter, first find distance between points





so, perimeter is:
if







draw two diagonals and cut polygon into three triangles



use Heron's Formula for the area of a triangle:
 where where where where is half the perimeter, or is half the perimeter, or

the area of triangle 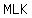 is: is:
if  , ,  , , 








the area of triangle  is: is:









the area of triangle 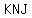 is: is:









so the total area is:


 ≈ ≈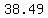
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
To find the perimeter, there are no shortcuts; you just need to use the distance formula (aka Pythagorean Theorem) to find the length of each side and find the sum. If an approximate answer is okay, then use decimal approximations, as the other tutor did. If an exact answer is required, leave the length of each side in radical form.
For the area, there are two methods I know that are less work than the method show by the other tutor (dividing the figure into three triangles and using Heron's formula three times to find the area of each).
One way is to enclose the figure in a rectangle and find the area of the figure as the area of that rectangle minus the areas of the triangular regions outside the figure and inside the rectangle.

The area is ABCD - (ALK + BKJ + CJN + DML) = 48-(2+3+2.5+2) = 38.5
For this figure, that method was not too bad, because we only had to subtract the areas of four triangles from the area of the surrounding rectangle. In more complicated figures, that method becomes quite difficult to use.
Here is a method that can be used to quickly find the area of any polygon.
(1) Make a list of the coordinates of the given points, making sure the list is in an order so that the points connected in that order form a polygon; repeat the first point at the bottom of the list (I used LKJNML):
-4 1
-2 3
4 2
3 -3
-3 -3
-4 1
Form the products, diagonally down left to right; and find their sum:
-4 1
\
-2 3
\ \
4 2 -12
\ \
3 -3 -4
\ \
-3 -3 -12
\ \
-4 1 -9
\
-3
----
-40
Form the products, diagonally down right to left; and find their sum:
-4 1
/
-2 3
/ /
-2 4 2
/ /
12 3 -3
/ /
6 -3 -3
/ /
9 -4 1
/
12
----
37
The area of the polygon is the absolute value of one-half the difference between the two sums:

This method can be used to quickly find the area of any polygon, given the coordinates of the vertices.
When pencil and paper are used to find the two sets of sums, you end up with the crossed "\" and "/" symbols in the middle, giving the popular name "shoelace method" to this method.
|
|
|