.
The angles of polygon are in arithmetic expression 172°,168° and 164°. How many sides does the polygon have?
~~~~~~~~~~~~~~~~~~~~~~
Your formulation is not perfect, unfortunately.
The correct formulation is this:
The angles of polygon are in arithmetic progression 172°,168°, 164° and so on . . . .
How many sides does the polygon have?
Solution
The corresponding sequence of exterior angles is 8°, 12°, 16° and so on . . .
It is an arithmetic progression with the first term of 8 and the common difference of 4.
The sum of exterior angles of any (convex) polygon is 360°.
So, you need to find "n", the number of sides/vertices, from the condition
= 360°, where is the sum of the first n terms of this AP.
You can use the formula for = 
,
which gives you an equation
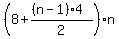= 360, or, which is the same
(8 + 2*(n-1))*n = 360.
It reduces to a quadratic equation
2n^2 + 6n - 360 = 0, which is equivalent to
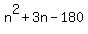= 0.
It can be solved by factoring
(n-12)*(n+15) = 0,
which gives you only one positive solution n = 12.
Answer. n= 12. The polygon has 12 sides.
