This Lesson (Upper level combinatorics problem on subsets of a finite set) was created by by ikleyn(53107)   : View Source, ShowAbout ikleyn:
Upper level combinatorics problem on subsets of a finite set
Problem 1Let S = {1, 2, 3, 4, . . . , n}, and let A and B be two subsets of S such that A ≠ ∅, B ≠ S, and A ⊆ B.
Calculate the number of ordered pairs (A,B) for all subsets of the set S.
Solution
Set S contains n distinguishable elements.
Let m be an integers number 0 <= m <= n.
The number of different subsets B in S, consisting of m elements, is  .
Notice that in this formula, I admit B = S. This case will be excluded later.
So, for given integer m between 1 and n, we can choose subset B in .
Notice that in this formula, I admit B = S. This case will be excluded later.
So, for given integer m between 1 and n, we can choose subset B in  different ways.
Let B is one such selected set of m elements.
The number of all different subsets A in B is different ways.
Let B is one such selected set of m elements.
The number of all different subsets A in B is 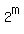 .
Notice that in this formula, I admit A = ∅. This case will be excluded later.
Having this, we conclude that the number of all pairs (A,B), where A is a subset in B, is .
Notice that in this formula, I admit A = ∅. This case will be excluded later.
Having this, we conclude that the number of all pairs (A,B), where A is a subset in B, is
 .
This sum is REMARCABLE. It is nothing else as .
This sum is REMARCABLE. It is nothing else as 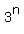 . Indeed, this sum is a binomial expansion/decomposition,
which can be folded back . Indeed, this sum is a binomial expansion/decomposition,
which can be folded back
 = = 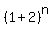 = = 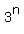 .
OK. The problem is almost fully solved. To fully complete it, we only need to exclude all pairs
(A,B), where B = S or A = ∅.
The number of pairs (A,S) is the same as the number of all subsets A in S: it is .
OK. The problem is almost fully solved. To fully complete it, we only need to exclude all pairs
(A,B), where B = S or A = ∅.
The number of pairs (A,S) is the same as the number of all subsets A in S: it is 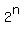 , including the subset (∅,S).
The number of pairs (∅,B) is the same as the number of subsets B in S: it is , including the subset (∅,S).
The number of pairs (∅,B) is the same as the number of subsets B in S: it is 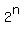 again,
including the subset (∅,S).
So, when we exclude the prohibited pairs, we will get
the number of all pairs under the problem's question is again,
including the subset (∅,S).
So, when we exclude the prohibited pairs, we will get
the number of all pairs under the problem's question is 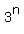 - - 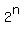 - - 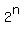 + 1 = + 1 = 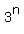 - - 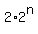 + 1.
I added 1 to compensate the fact that above I excluded the pair (∅,S) twice.
ANSWER. The number of all pairs under the problem's question is + 1.
I added 1 to compensate the fact that above I excluded the pair (∅,S) twice.
ANSWER. The number of all pairs under the problem's question is 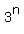 - - 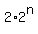 + 1. + 1.
Now the problem is solved completely.
My other additional lessons on Combinatorics problems in this site are
- Upper league combinatorics problem
- Upper level problems on a party of people sitting at a round table
- A confusing combinatorics problem on repeating digits in numbers
- Upper level combinatorics problems on Inclusion-Exclusion principle
- This nice problem teaches to distinguish permutations from combinations
- OVERVIEW of additional combinatorics problems
Use this file/link ALGEBRA-II - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-II.
This lesson has been accessed 682 times.
|

