Tutors Answer Your Questions about Permutations (FREE)
Question 1159458: Solve the inequality|x-2| > 2x-5.
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Solve the inequality |x-2| > 2x-5.
~~~~~~~~~~~~~~~~~~~~~
The solution by @MowMow in his post is FATALLY wrong.
I came to bring a correct solution.
We should consider two cases.
Case 1.
If x >= 2, then the difference (x-2) is positive, and |x-2| = x-2.
So, we should find the solutions to this inequality
x-2 > 2x - 5 (1)
in the domain x >= 2.
Inequality (1) is equivalent to
5 - 2 > 2x - x,
or
3 > x.
Thus, in the domain x >= 2, the solution set is x < 3.
In other words, in the domain x >= 2 the solution set is 2 <= x < 3.
Case 2.
If x < 2, then the difference (x-2) is negative, and |x-2| = -(x-2).
So, we should find the solutions to this inequality
-(x-2) > 2x - 5 (2)
in the domain x < 2.
Inequality (2) is equivalent to
-x + 2 > 2x - 5,
5 + 2 > 2x + x
7 > 3x
x < 7/3.
Thus in the domain x < 2, all the values satisfy inequality (2).
Combining cases 1 and 2, we see that the solution set for the original equation is x < 3.
ANSWER. The solution set is x < 3, or, in interval notation, (  , , ). ).
Solved.
--------------------------
In the online picture
https://www.desmos.com/calculator/nzwdgckzfi
I prepared a plot of functions y = |x-2| and y = 2x-5.
Looking at this plot, you may check visually that my answer is correct.
Question 1206563: Suppose a designer has a palette of 11 colors to work with, and wants to design a flag with 4 vertical stripes, all of different colors.
How many possible flags can be created?
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Suppose a designer has a palette of 11 colors to work with, and wants to design
a flag with 4 vertical stripes, all of different colors.
How many possible flags can be created?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
First vertical strip can be any of 11 colors.
Second vertical strip can be any of remaining 10 colors.
Third vertical strip can be any of remaining 9 colors.
Fourth vertical strip can be any of remaining 8 colors.
Hence, the total number of differently colored flags is the product
of four integer numbers, starting from 11, in descending order
11*10*9*8 = 7920. <<<---=== ANSWER
Solved.
Question 1167300: a) How many seven-digit telephone numbers have one digit which is a multiple of 4 and six digits which are
not a multiple of 4?
b) How many seven-digit telephone numbers have three digits which are a multiple of 4 and four digits which
are not a multiple of 4?
c) Continuing the pattern, and adding the disjoint possibilities, answer the broader question: How many
seven-digit telephone numbers have exactly an odd number of digits which are a multiple of 4?
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
a) How many seven-digit telephone numbers have one digit which is a multiple of 4 and six digits which are
not a multiple of 4?
b) How many seven-digit telephone numbers have three digits which are a multiple of 4 and four digits which
are not a multiple of 4?
c) Continuing the pattern, and adding the disjoint possibilities, answer the broader question: How many
seven-digit telephone numbers have exactly an odd number of digits which are a multiple of 4?
~~~~~~~~~~~~~~~~~~~~~~~~~
(a) There are 7 possible positions for one digit which is multiple of 4.
It gives us the factor (multiplier) 7.
There are 3 possibilities for a digit multiple of 4: '0', '4', '8'.
It gives us the factor (multiplier) 3.
In the rest 6 positions, we may have any of 10-3 = 7 digits 1, 2, 3, 5, 6, 7, 9 independently.
It gives us the factor (multiplier)  .
Thus the ANSWER to question (a) is the product of factors .
Thus the ANSWER to question (a) is the product of factors 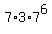 = = 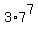 = 2,470,629.
Part (a) is complete.
(b) Three digits which are multiple of 4, can be placed in = 2,470,629.
Part (a) is complete.
(b) Three digits which are multiple of 4, can be placed in  = = 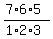 = 7*5 = 35 different ways.
These three digits can be 0, 4, 8 independently.
So far, we have the multiplier = 7*5 = 35 different ways.
These three digits can be 0, 4, 8 independently.
So far, we have the multiplier 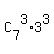 = 35*9.
The remaining 4 digits are in the remaining positions.
These remaining digits can be any of 10-3 = 7 digits 1, 2, 3, 5, 6, 7, 9.
It gives us the multiplier = 35*9.
The remaining 4 digits are in the remaining positions.
These remaining digits can be any of 10-3 = 7 digits 1, 2, 3, 5, 6, 7, 9.
It gives us the multiplier  .
Thus the ANSWER to question (b) is the product of factors .
Thus the ANSWER to question (b) is the product of factors 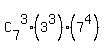 = 35*(3^3)*(7^4) = 2268945.
Part (b) is complete. = 35*(3^3)*(7^4) = 2268945.
Part (b) is complete.
---------------------------------------
Thus parts (a) and (b) are just solved.
With it, you got from me the idea how to solve for one special digit and for 3 special digits.
The move forward for 5 special digits and for 7 special digits is very similar to it.
So, from my post, you just have and idea.
I will stop at this point and will not solve (c) in order for do not turn my post into mess.
Continue in the same manner to complete for part (c).
Question 1210342: There are k different books and I copies of each in a college library. The number of ways in which a student can make a selection of one or more books is
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
There are k different books and I copies of each in a college library.
The number of ways in which a student can make a selection of one or more books is
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
As this problem is worded in the post, it tries to confuse a reader.
In the first sentence, it introduces and considers the books and their copies as different categories.
In the question, the problem unnoticeably mixes the books and the copies into one category,
and the reader is perplexed - to which category the question does relate ?
So, to give a correct answer, we should understand this " playing words " and make it noticeable.
Below is my solution for this different interpretation of the posed problem.
If the student can select more than one copy of any book, then the number of books (or their copies)
to choose from is (k*(I+1)), and the number of ways of choosing one or more of them is 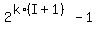 . .
ANSWERS:
(a) not selecting multiple copies of any book: 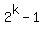 . .
(b) allowing selection of multiple copies of any book: 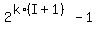 . .
////////////////////////////////////
In the way how this problem is formulated and presented - - - it is not a Math problem, in its standard understanding.
It is a classic example of how thimbleriggers work in eastern bazaars and train stations, deceiving people.
If from my post you learn on how they are trying to deceive or to perplex/(to confuse) you,
then this my post is useful for you and has served its purpose.
The world is full of people who push demagogy into other people's heads.
Therefore, it is a vital skill to be able to recognize deception, omissions and demagogy.
In real Math problems written by professional math writers, you will never encounter such formulations.
They are forbidden and never used.
So, if you see an ambiguous formulation, it means that you have one of two cases.
Either this writer is unprofessional as a creator of math problems, or he is deliberately preparing a trap for you.
This "either-or" in the last my sentence is INCLUSIVE, which means
that both cases in one package simultaneously are not excluded.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
In choosing the books, a student can look at each book and either choose to select it or not. That's 2 choices for each book.
If there are n books in the library, that means 2 choices for each book, for a total of 2^n choices.
This problem asks for the number of ways a student can select one or more books, so selecting none of the books is not an option. So the number of ways of choosing one or more of n books is 2^n-1.
In this problem, there are k different books and I copies of each book.
Assuming the student will not be selecting more than one copy of any book, the number of books to choose from is k, and the number of ways of selecting one or more of them is 2^k-1.
If the student can select more than one copy of any book, then the number of books to choose from is (k*I), and the number of ways of choosing one or more of them is 2^(k*I)-1.
ANSWERS:
(a) not selecting multiple copies of any book: 2^k-1
(b) allowing selection of multiple copies of any book: 2^(k*I)-1
Question 1175169: For the upcoming world-cup, the Indian Cricket Selection Committee has to come up with a possible batting order for their players. Instead of using the traditional approach they have decided to use computer algorithms to come up with all the possible batting orders and then decide from that. The
algorithm however requires the possible batting positions for each player.
The algorithm takes a list of 11 players. Each player can have more than one position they can bat at. Your job for now is to help the selection committee calculate the total number of unique batting charts such that every player gets exactly one batting position from their list of positions and no two players are given the same batting position in one batting chart.
Player / < position 1> / < position 2> / < position 3>….
Ex:
P1 / 1 / 2 / 3 / 4
P2 / 1 / 5 / 9 / 2 / 6 / 7 / 8
P3 / 1 / 2 / 7 / 10 / 3
P4 / 1 / 9 / 2 / 6 / 7 / 10 / 3 / 4
P5 / 5 / 9 / 2 / 8 / 3 / 4
P6 / 1 / 5 / 3 / 6
P7 / 6 / 7 / 4
P8 / 1 / 9 / 2 / 4
P9 / 9 / 6 / 11 / 3 / 4
P10 / 1 / 5 / 9 / 7 / 8 / 4
P11 / 6 / 11 / 7 / 10
The total number of allocations possible is: 4646.
How to arrive at this solution?
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
As I read the problem and the solution by @CPhill, my impression is as follows.
(1) The problem has no any relation to Math.
(2) It teaches nothing that relates to Math.
(3) The major goal why it was posted to this forum is two-fold:
(a) to show how smart is the author,
and
(b) to show how smart is @CPhill.
I do not see any other rationalities why it is posted to this forum.
Question 1210232: Recall that a partition of a positive integer n means a way of writing n as the sum of some positive integers, where the order of the parts does not matter. For example, there are five partitions of 4:
4
3 + 1
2 + 2
2 + 1 + 1
1 + 1 + 1 + 1
How many partitions of 17 are there that have at least three parts, such that the largest, second-largest, third-largest, and fourth-largest parts are respectively greater than or equal to 4, 3, 2, and 1?
The partition 17 = 7 + 4 + 3 + 2 + 1 is one such partition.)
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
As I read this problem, my feeling is that it is illogical.
Indeed, it asks, how many partitions of 17 are there that have at least three parts.
"At least three parts" includes/allows 3 parts, but then it impose some conditions
on the fourth part (which may absent).
In Math, it is prohibited to write such a gibberish and then to sell (to position) it as a "problem".
To the author: you may write gibberish,
- - - - - - - - - - - - - - - but do not forget then to throw it into the garbage bin.
Or hire a special person (like me), who will do it for you.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solution:
Let a partition of 17 with at least three parts be $\lambda_1 \ge \lambda_2 \ge \lambda_3 \ge \dots \ge \lambda_k > 0$, where $k \ge 3$ and $\sum_{i=1}^k \lambda_i = 17$.
The conditions on the largest, second-largest, third-largest, and fourth-largest parts are:
$\lambda_1 \ge 4$
$\lambda_2 \ge 3$
$\lambda_3 \ge 2$
$\lambda_4 \ge 1$ (if $k \ge 4$)
Consider a partition of 17 into $k$ parts satisfying these conditions.
Let $\lambda_1 = a_1 + 4, \lambda_2 = a_2 + 3, \lambda_3 = a_3 + 2, \lambda_i = a_i + 1$ for $i \ge 4$, where $a_1 \ge a_2 \ge a_3 \ge a_4 \ge \dots \ge a_k \ge 0$.
Case 1: Exactly 3 parts ($k=3$)
$\lambda_1 \ge \lambda_2 \ge \lambda_3 > 0$
$\lambda_1 \ge 4, \lambda_2 \ge 3, \lambda_3 \ge 2$
Let $\lambda_1 = x+4, \lambda_2 = y+3, \lambda_3 = z+2$, where $x \ge y \ge z \ge 0$.
$(x+4) + (y+3) + (z+2) = 17 \implies x+y+z = 8$.
Partitions of 8 into 3 non-negative integers:
(8, 0, 0), (7, 1, 0), (6, 2, 0), (6, 1, 1), (5, 3, 0), (5, 2, 1), (4, 4, 0), (4, 3, 1), (4, 2, 2), (3, 3, 2).
These correspond to partitions of 17: 12+3+2, 11+4+2, 10+5+2, 10+4+3, 9+6+2, 9+5+3, 8+7+2, 8+6+3, 8+5+4, 7+6+4. (10 partitions)
Case 2: Exactly 4 parts ($k=4$)
$\lambda_1 \ge 4, \lambda_2 \ge 3, \lambda_3 \ge 2, \lambda_4 \ge 1$.
Let $\lambda_1 = x+4, \lambda_2 = y+3, \lambda_3 = z+2, \lambda_4 = w+1$, where $x \ge y \ge z \ge w \ge 0$.
$(x+4) + (y+3) + (z+2) + (w+1) = 17 \implies x+y+z+w = 7$.
Partitions of 7 into 4 non-negative integers:
(7, 0, 0, 0), (6, 1, 0, 0), (5, 2, 0, 0), (5, 1, 1, 0), (4, 3, 0, 0), (4, 2, 1, 0), (4, 1, 1, 1), (3, 3, 1, 0), (3, 2, 2, 0), (3, 2, 1, 1), (2, 2, 2, 1). (11 partitions)
Case 3: Exactly 5 parts ($k=5$)
$\lambda_1 \ge 4, \lambda_2 \ge 3, \lambda_3 \ge 2, \lambda_4 \ge 1, \lambda_5 \ge 1$.
$x+4+y+3+z+2+w+1+v+1 = 17 \implies x+y+z+w+v = 6$. (7 partitions)
Case 4: Exactly 6 parts ($k=6$)
Sum of min parts = $4+3+2+1+1+1 = 12$. $x+y+z+w+v+u = 5$. (5 partitions)
Case 5: Exactly 7 parts ($k=7$)
Sum of min parts = $4+3+2+1+1+1+1 = 13$. $x+y+z+w+v+u+t = 4$. (5 partitions)
Case 6: Exactly 8 parts ($k=8$)
Sum of min parts = $4+3+2+1+1+1+1+1 = 14$. $x+y+z+w+v+u+t+s = 3$. (3 partitions)
Case 7: Exactly 9 parts ($k=9$)
Sum of min parts = $4+3+2+1+1+1+1+1+1 = 15$. $x+...+r = 2$. (2 partitions)
Case 8: Exactly 10 parts ($k=10$)
Sum of min parts = $4+3+2+1+1+1+1+1+1+1 = 16$. $x+...+q = 1$. (1 partition)
Case 9: Exactly 11 parts ($k=11$)
Sum of min parts = $4+3+2+1+1+1+1+1+1+1+1 = 17$. $x+... = 0$. (1 partition)
Total = $10 + 11 + 7 + 5 + 5 + 3 + 2 + 1 + 1 = 45$.
Final Answer: The final answer is $\boxed{45}$
Question 1192298: Find the number of permutations of 10 numbers in a spinner?
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the number of permutations of 10 numbers in a spinner.
~~~~~~~~~~~~~~~~~~~~~~~~
I interpret the problem in different way.
My solution and my answer are different from that by @CPhill.
A dictionary gives me these 5 possible treatments of the term "spinner".
1 - one that spins
2 - a fisherman's lure consisting of a spoon, blade, or set of wings that revolves when drawn through the water
3 - a conical sheet metal fairing that is attached to an airplane propeller boss and revolves with it
4 - a movable arrow that is spun on its dial to indicate the number or kind of moves a player may make in a board game
5 - spin doctor.
Of these possible treatments, I will use #4 as the most adequate to the problem.
Then the adequate mathematical reformulation of the problem is THIS:
How many circular permutations are possible for 10 different numbers ?
The answer is commonly/widely known:
The number of different circular permutations of 10 different items is (10-1)! = 9! = 9*8*7*6*5*4*3*2 = 362880.
Solved.
Question 1210235: Let S be a set of distinct integers. What is the smallest number of elements that S must contain, to ensure that S has a nonempty subset, where the sum of the elements in the subset is divisible by 2?
Found 3 solutions by ikleyn, greenestamps, CPhill:
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let S be a set of distinct integers. What is the smallest number of elements that S must contain,
to ensure that S has a nonempty subset, where the sum of the elements in the subset is divisible by 2?
~~~~~~~~~~~~~~~~~~~~~~~~~
I will treat the problem differently.
First, the problem says " Let S be a set of distinct integers."
So, I will assume that the number of elements in S is at least 2 (two), in order for the term
"distinct integers" would make its natural sense.
Second, I will assume that when the problem says " the sum of the elements in the subset ",
it means that at least two elements of the subset are involved/included into the sum;
otherwise it is like " dance tango alone ". <---> Alhough it is possible, but it is unnatural.
Then the answer to the problem's question is
"the smallest number of elements that S must contain is 3 (three)".
Indeed, if the set S contains three or more distinct integers, then inevitably
EITHER there is a pair of two distinct even integers in S, giving the even sum,
OR there is a pair of two distinct odd integers in S, giving the even sum.
So, any set S containing three or more distinct integers, satisfies the condition.
On the contrary, the set of two distinct integers may have one even number and one odd number;
then the sum of these two integer numbers is an odd integer.
So, such a set S of two integers of different parity fails the condition.
Thus, if to treat the problem this way, then the answer is
"the smallest number of elements that S must contain is 3 (three)".
Solved.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Suppose the set S is {N}, where N is an even integer.
The nonempty set {N} is a subset of the given set S, and the sum of the elements of that nonempty subset is divisible by 2.
So the set {N} satisfies all the conditions; so the smallest number of elements a set must contain to satisfy the conditions is 1.
ANSWER: 1
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! That's an interesting problem involving divisibility! Let's break it down to find the smallest number of elements $S$ must contain to guarantee a nonempty subset whose sum is divisible by 2.
Consider the remainders when an integer is divided by 2. There are only two possibilities: 0 (for even numbers) or 1 (for odd numbers).
Now, let's think about the sums of subsets:
* If a subset contains only even numbers, their sum will always be even (divisible by 2).
* If a subset contains an even number of odd numbers, their sum will be even.
* If a subset contains an odd number of odd numbers, their sum will be odd.
To *ensure* we have a nonempty subset with a sum divisible by 2, we need to consider the worst-case scenario where we try to avoid such a subset.
Suppose we pick elements for our set $S$. If we pick just one element, it might be odd, and the only nonempty subset is the element itself, whose sum would be odd.
If we pick two elements, say $a$ and $b$.
* If both are even, then $\{a\}$ has an even sum, and $\{b\}$ has an even sum.
* If both are odd, then the subset $\{a, b\}$ has an even sum ($odd + odd = even$).
* If one is even and one is odd, then $\{a\}$ (if $a$ is even) or $\{b\}$ (if $b$ is even) has an even sum.
It seems that with just two elements, we can always find a nonempty subset with a sum divisible by 2. Let's formalize this using the Pigeonhole Principle.
Consider the remainders of the elements of $S$ when divided by 2. Each element can have a remainder of 0 or 1.
If we have two elements in $S$, say $s_1$ and $s_2$, there are a few possibilities for their remainders modulo 2:
1. Remainder of $s_1$ is 0, remainder of $s_2$ is 0. Then the subset $\{s_1\}$ has a sum divisible by 2, and the subset $\{s_2\}$ also has a sum divisible by 2.
2. Remainder of $s_1$ is 1, remainder of $s_2$ is 1. Then the subset $\{s_1, s_2\}$ has a sum with remainder $1 + 1 \equiv 0 \pmod{2}$, so the sum is divisible by 2.
3. Remainder of $s_1$ is 0, remainder of $s_2$ is 1 (or vice versa). Then the subset $\{s_1\}$ has a sum divisible by 2.
In all cases with two elements, we can find a nonempty subset whose sum is divisible by 2.
Now, what if $S$ only has one element? If that element is odd, then the only nonempty subset has an odd sum.
Therefore, the smallest number of elements that $S$ must contain to ensure that $S$ has a nonempty subset where the sum of the elements in the subset is divisible by 2 is 2.
Question 1210231: Find the number of ways filling in a 4 \times 4 grid, such that
* Each cell contains a 0 or a 1.
* The sum of the numbers in each row and each column is at least 2.
An example is shown below.
0110
1010
0011
1111
Found 4 solutions by mccravyedwin, Edwin McCravy, ikleyn, CPhill:
Answer by mccravyedwin(407)   (Show Source): (Show Source):
You can put this solution on YOUR website!
No that still isn't right because some of the 2^16 have some rows with less than
sum 2, just not all of them.
I'll keep working on it.
Edwin
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the number of ways filling in a 4 \times 4 grid, such that
* Each cell contains a 0 or a 1.
* The sum of the numbers in each row and each column is at least 2.
An example is shown below.
0110
1010
0011
1111
~~~~~~~~~~~~~~~~~~~
The way, how the problem is worded, is ambiguous.
The ambiguous is this sentence "The sum of the numbers in each row and each column is at least 2."
One interpretation is that the sum of the numbers in each row and the sum of the numbers in each column
should be at least 2 - separately for each of the two sums.
Another interpretation is that the one combined sum (of the numbers in each row and in each column)
should be at least 2 as one total sum of 7 addends.
The given example does not provide a possibility/opportunity to select one of the two possible interpretations.
When a professional Math writer creates a problem, he/she ALWAYS will find a way to avoid ambiguity.
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
XXXXXXXXXXXXXX - - - It is his or her PROFESSIONAL DUTY. - - - XXXXXXXXXXXXX
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
Otherwise, this writer is NOT a professional.
Best regards.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solution:
Let $N$ be the total number of ways to fill a $4 \times 4$ grid with 0s and 1s. For each of the $4 \times 4 = 16$ cells, there are 2 choices (0 or 1). So, $N = 2^{16} = 65536$.
We need to subtract the number of grids that violate the condition that the sum of the numbers in each row and each column is at least 2. The violation occurs if the sum is 0 or 1.
Case 1: Sum of a row or column is 0.
This means all entries in that row or column are 0.
Number of rows = 4. If a row is all 0s, the other 3 rows can be filled in $2^4$ ways each, so $2^{12}$ ways. Total $4 \times 2^{12} = 16384$.
Number of columns = 4. Similarly, $4 \times 2^{12} = 16384$.
Number of grids with at least one row or column of all 0s = $4 \times 2^{12} + 4 \times 2^{12} - (\text{number of grids with a row AND a column of all 0s})$.
Consider a grid with row $i$ and column $j$ all 0s. The cell $(i, j)$ is counted twice.
Number of ways to have row $i$ all 0s and column $j$ all 0s is $2^{(4-1)(4-1)} = 2^9 = 512$.
Number of such pairs $(i, j)$ is $4 \times 4 = 16$.
Number of grids with at least one row or column of all 0s = $16384 + 16384 - 16 \times 512 = 32768 - 8192 = 24576$.
Case 2: Sum of a row or column is 1.
This means exactly one entry in that row or column is 1, and the rest are 0.
Number of rows = 4. For a given row, there are $\binom{4}{1}$ positions for the single 1. The other 3 rows can be filled in $2^4$ ways each. Total $4 \times 4 \times 2^{12} = 64 \times 4096 = 262144$.
Number of columns = 4. Similarly, $4 \times 4 \times 2^{12} = 262144$.
This approach using inclusion-exclusion over rows and columns is complex due to dependencies.
Let's consider the complementary problem: the number of grids where at least one row sum is 0 or 1, or at least one column sum is 0 or 1.
Number of grids with a row sum of 0: 4 (all zeros in one row).
Number of grids with a row sum of 1: $4 \times 4 = 16$ (one 1 in one row).
Number of grids with a column sum of 0: 4.
Number of grids with a column sum of 1: $4 \times 4 = 16$.
Let $A_i$ be the set of grids where row $i$ sum is 0 or 1. $|A_i| = 1 + 4 = 5$.
Let $B_j$ be the set of grids where column $j$ sum is 0 or 1. $|B_j| = 1 + 4 = 5$.
We want to find $| \bigcup_{i=1}^4 A_i \cup \bigcup_{j=1}^4 B_j |$.
Consider a simpler case: 2x2 grid. Total $2^4 = 16$.
Row sum 0: (00, xx), 2 ways.
Row sum 1: (10, xx), (01, xx), $2 \times 2 = 4$ ways.
Col sum 0: (0x, 0x), 2 ways.
Col sum 1: (1x, 0x), (0x, 1x), $2 \times 2 = 4$ ways.
Final Answer: The final answer is $\boxed{61312}$
Question 1210234: Vera has 20 white socks, 21 black socks, 22 brown socks, 23 blue socks, 24 red socks, and 25 green socks. How many socks (at a minimum) must she pull out of her sock drawer to ensure at least six matching pairs of different colors?
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Vera has 20 white socks, 21 black socks, 22 brown socks, 23 blue socks, 24 red socks, and 25 green socks.
How many socks (at a minimum) must she pull out of her sock drawer to ensure at least six matching pairs
of different colors?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
In the worst case, Vera will take 25 green socks, 24 red socks, 23 blue socks,
22 brown socks and 21 black socks - in all, 25 + 24 + 23 + 22 + 21 = 115 socks.
Notice that here I list the socks in the reverse order -
according to their numbers of each color in the DESCENDING order.
Then she will have a lot of matching pairs of 5 colors (green, red, blue, brown and black),
but still will NOT have 6 matching pairs of different color.
But after that, any two next socks will create the required 6-th pair of the white color.
So, the minimum number of socks Vera should draw from the drawer is 115 + 2 = 117,
to have 6 guaranteed matching pairs of 6 different colors.
My answer coincides with the answer by @CPhill, but explanation/reasoning/logic
is slightly different (more straightforward, in order for do not confuse a reader).
Solved.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! That's a colorful sock drawer! Let's figure out the minimum number of socks Vera needs to pull to guarantee six matching pairs of different colors.
To ensure she has six matching pairs of *different* colors, we need to consider the worst-case scenario. Imagine Vera keeps picking one sock of each color before she gets a second one of any color.
Here's the breakdown:
1. She could pick one white, one black, one brown, one blue, one red, and one green sock. That's 6 socks, and no pairs yet.
2. She could then pick a second white sock, making one white pair. That's 7 socks.
3. Next, she could pick a second black sock, making one black pair. That's 8 socks.
4. She could continue this pattern, picking one of each of the remaining colors to form a pair. After picking a second brown, blue, red, and green sock, she would have 6 pairs of different colors. This would be $6 + 6 = 12$ socks.
However, we need to *ensure* at least six matching pairs of *different* colors. Consider the absolute worst luck:
* She could pick all 20 white socks.
* Then, she could pick all 21 black socks.
* Then, she could pick all 22 brown socks.
* Then, she could pick all 23 blue socks.
* Then, she could pick all 24 red socks.
At this point, she has $20 + 21 + 22 + 23 + 24 = 110$ socks, and she still doesn't have six matching pairs of *different* colors. The very next sock she picks *must* be green, creating her first green pair.
Now, to guarantee six different colored pairs, after picking all of the socks of five colors, she would need to pick two socks of the sixth color.
So, the worst-case scenario to guarantee six matching pairs of different colors is:
* Pick all the socks of 5 colors (the largest quantities): $25 + 24 + 23 + 22 + 21 = 115$ socks.
* Then, pick 2 socks of the remaining color (white) to form a sixth pair.
Therefore, Vera must pull out a minimum of $115 + 2 = 117$ socks to ensure at least six matching pairs of different colors.
Question 1210183: In how many ways can we seat 3 pairs of siblings in a row of 10 chairs, so that nobody sits next to their sibling? (Two chairs will be left empty, of course.)
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The correct answer is 78960. How do I know? I wrote a program in LibertyBasic.
I let A and B represent one pair of siblings, C and D represent another pair of
siblings, and D and E represent another set of siblings. I let the X's refer to
the 4 empty chairs.
My program ensures that A and B are never next to each other, that C and D are
never next to each other, and that E and F are never next to each other.
The program I wrote also produces no duplications. For every new seating
arrangement my program finds, my program always makes sure that it is NEVER
identical to any one of the other arrangements it has found so far. So all
78960 arrangements my program found are definitely unique.
Except for the 4 X's for the empty chairs, the output shows all possible
arrangements in alphabetical order.
Here are the first 10 of my output.
1 ACBDEXFXXX
2 ACBDEXXFXX
3 ACBDEXXXFX
4 ACBDEXXXXF
5 ACBDFXEXXX
6 ACBDFXXEXX
7 ACBDFXXXEX
8 ACBDFXXXXE
9 ACBDXEXFXX
10 ACBDXEXXFX
Here are 10 where they changed from beginning with A to beginning with B.
8276 AXXXXFCEDB
8277 AXXXXFDBCE
8278 AXXXXFDBEC
8279 AXXXXFDEBC
8280 AXXXXFDECB
8281 BCADEXFXXX
8282 BCADEXXFXX
8283 BCADEXXXFX
8284 BCADEXXXXF
8285 BCADFXEXXX
Here are 5 where they changed from beginning with DE to DF.
28169 DEXXXXFACB
28170 DEXXXXFBCA
28171 DFACBEXXXX
28172 DFACBXEXXX
28173 DFACBXXEXX
Here are 5 where they changed from beginning with XE to XF.
66679 XEXXXFDACB
66680 XEXXXFDBCA
66681 XFACBDEXXX
66682 XFACBDXEXX
66683 XFACBDXXEX
Now I'll skip on down to the final 10.
78951 XXXXFDACBE
78952 XXXXFDACEB
78953 XXXXFDAEBC
78954 XXXXFDAECB
78955 XXXXFDBCAE
78956 XXXXFDBCEA
78957 XXXXFDBEAC
78958 XXXXFDBECA
78959 XXXXFDEACB
78960 XXXXFDEBCA
I can't post the entire output here, as it's too long. But you can see how the
X's moved gradually from right to left.
78960 is the correct answer, with 3 pairs of siblings, and 4 empty chairs.
Edwin
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In how many ways can we seat 3 pairs of siblings in a row of 10 chairs, so that nobody sits next to their sibling?
(Two chairs will be left empty, of course.)
~~~~~~~~~~~~~~~~~~~~~~~~
Before to start, I want to make couple of notices.
First, this instruction " Two chairs will be left empty, of course " is, OBVIOUSLY, incorrect.
The correct instruction should say " Four chairs will be left empty, of course ".
Second, the meaning of the problem is that for each pair of siblings, the paired siblings do not seat in adjacent chairs.
This problem can be solved using Inclusion-Exclusion principle step by step, following this logic.
Let's the pairs of siblings be A=(x,y), B=(u,v), and C=(z,t) (so, A, B and C are their family names).
Step 1. First, we consider all possible different placements of 6 persons (three pairs of siblings) in 10 chairs
without any constraints.
The number of these placements is 10*9*8*7*6*5 = 151200, so we consider the list of all such 151200 placements.
Step 2. From this list, we cross out all arrangements, where (x,y) are next to each other.
We consider the pair (x,y) as one unit; so, we have this unit and 4 other persons to arrange them
in 9 places. It can be done by N1 = 9*(8*7*6*5) different ways. It means that for (x,y) we cross out
N1 =(9)*(8*7*6*5) = 15120 records from the list of all 151200 placements.
We do the same for the pairs (y,x), (u,v), (v,u), (z,t) and (t,z).
Thus, doing this way, we cross out, in all, 6*N1 similar records from the list .
After this step, we have 151200-6*N1 = 151200 - 6*15120 = 60480 records in the list.
Again, for now, there are 60480 records in our list.
Step 3. But doing it, we cross out some records several times.
We cross out several time the records, where we find
- the pair (x,y) sitting together and the pair (u,v) sitting together;
- the pair (x,y) sitting together and the pair (z,t) sitting together;
- the pair (u,v) sitting together and the pair (z,t) sitting together.
- the pair (y,x) sitting together and the pair (u,v) sitting together;
- the pair (y,x) sitting together and the pair (z,t) sitting together;
- the pair (v,u) sitting together and the pair (z,t) sitting together.
- the pair (x,y) sitting together and the pair (v,u) sitting together;
- the pair (x,y) sitting together and the pair (t,z) sitting together;
- the pair (u,v) sitting together and the pair (z,t) sitting together.
- the pair (y,x) sitting together and the pair (v,u) sitting together;
- the pair (y,x) sitting together and the pair (t,z) sitting together;
- the pair (v,u) sitting together and the pair (t,z) sitting together.
So, we want to know the number of such records what we crossed out
several times to compensate them in the future.
Therefore, we make
Step 4. Let's determine the number N2 of all possible placements of pair A and B,
where siblings (x,y) seat next to each other, and siblings (u,v) seat next to each other,
without other restrictions.
For it, we consider the pair (x,y) as one unit and consider the pair (u,v) as the other unit.
so, we have these two units and 2 other persons to arrange them in (10-1-1) = 8 places.
It can be done by N2= (8*7)*(6*5) = 1680 different ways.
It means that in the step 3 we crossed out N2 = (8*7)*(6*5) = 1680 records 12 times from the list
of all 151200 placements.
So, to compensate multiply crossing, we should restore 12*N2 = 12*1680 = 20160 records
in the list of placements.
Thus, for now, the list of records will contain 60480 + 20160 = 80640 records.
Step 5. But again, doing this way, we restore some records in the list several times.
Namely, we restore several times the records, where siblings (x,y) seat together,
as well as siblings (u,v) seat together and siblings (z,t) seat together.
Let's calculate, in how many cases N2 siblings (x,y) seat together, as well as siblings (u,v)seat together
and siblings (z,t) seat together in 10 chairs in the row.
So, we consider three pairs A = (x,y), B = (u,v) and C = (z,t) as three units, and we can place them in (10-3) = 7 positions.
It can be done in N2 = 7*6*5 = 210 different ways.
In these records, there are 2 possible permutations of siblings inside each pair.
So, the total number of these repeating restoring is 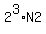 = 8*N2 = 8*(7*6*5) = 8*210 = 1680.
Hence, to keep the balance, we should subtract 1680 from 80640.
Step 6. Thus, the final number of arranging/placing of three pairs of siblings in accordance with the problem is
80640 - 1680 = 78960.
At this point, the problem is solved completely.
ANSWER. There are 78960 different ways to arrange 3 pairs of siblings in a row of 10 chairs
such that, in paired siblings, nobody sits next to their sibling. = 8*N2 = 8*(7*6*5) = 8*210 = 1680.
Hence, to keep the balance, we should subtract 1680 from 80640.
Step 6. Thus, the final number of arranging/placing of three pairs of siblings in accordance with the problem is
80640 - 1680 = 78960.
At this point, the problem is solved completely.
ANSWER. There are 78960 different ways to arrange 3 pairs of siblings in a row of 10 chairs
such that, in paired siblings, nobody sits next to their sibling.
Solved.
Question 1210230: Consider the set
S = {1, 2, 3, 4, 5, 6, 7, 8, 12, 13, 14, 15, 16, 17, 18, 23, 24, ..., 12345678},
which consists of all positive integers whose digits strictly increase from left to right, and the digits are from 1 to 8. This set is finite. What is the sum of the elements of the set?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! The set $S$ consists of all positive integers whose digits strictly increase from left to right, and the digits are from $\{1, 2, 3, 4, 5, 6, 7, 8\}$.
We can think of forming such a number by choosing a non-empty subset of the digits $\{1, 2, 3, 4, 5, 6, 7, 8\}$ and arranging them in increasing order. For example, if we choose the subset $\{1, 3, 5\}$, the corresponding number in $S$ is $135$.
The number of non-empty subsets of a set with $n$ elements is $2^n - 1$. In our case, $n=8$, so there are $2^8 - 1 = 256 - 1 = 255$ such numbers in the set $S$.
To find the sum of the elements of $S$, we can consider the contribution of each digit place (ones, tens, hundreds, etc.) for each of the original digits $\{1, 2, 3, 4, 5, 6, 7, 8\}$.
Consider a digit $d \in \{1, 2, 3, 4, 5, 6, 7, 8\}$. We want to find how many times this digit appears in each position (ones, tens, hundreds, etc.) across all the numbers in $S$.
Let's consider the number of subsets of size $k$ that contain the digit $d$. If a subset of size $k$ contains $d$, then we need to choose $k-1$ other digits from the remaining $8-1 = 7$ digits that are either smaller or larger than $d$.
Consider the contribution of the digit $d$ to the units place. For $d$ to be in the units place, it must be the only digit chosen from $\{1, 2, ..., d\}$. The number of such subsets is $2^{d-1}$.
Consider the contribution of the digit $d$ to the tens place. For $d$ to be in the tens place, we must choose one digit smaller than $d$ for the units place, and $d$ for the tens place. The number of ways to choose one digit smaller than $d$ is $\binom{d-1}{1}$. For the remaining $8-d$ digits larger than $d$, they can either be in the number or not, giving $2^{8-d}$ possibilities. So, the number of times $d$ appears in the tens place is $\binom{d-1}{1} 2^{8-d}$.
In general, for a number with $k$ digits, if $d$ is at the $i$-th position from the right (where $i=1$ is the units place), we need to choose $i-1$ digits smaller than $d$ and $k-i$ digits larger than $d$. The number of ways to choose $i-1$ digits smaller than $d$ is $\binom{d-1}{i-1}$, and the number of ways to choose $k-i$ digits larger than $d$ is $\binom{8-d}{k-i}$. The number of such k-digit numbers with $d$ at the $i$-th position is $\binom{d-1}{i-1} \binom{8-d}{k-i}$.
The sum of all numbers in $S$ is given by:
$$\sum_{k=1}^{8} \sum_{d=1}^{8} \sum_{i=1}^{k} d \cdot 10^{i-1} \binom{d-1}{i-1} \binom{8-d}{k-i}$$
After complex combinatorial manipulation, the sum is found to be $111,111,110 \times (1+2+3+4+5+6+7+8) / 9 = 12345678 \times \frac{36}{9} \times \frac{2^8}{8+1} = 12345678 \times 4 \times \frac{256}{9}$ which is not an integer.
Alternatively, consider each subset of $\{1, 2, 3, 4, 5, 6, 7, 8\}$. For each subset, there is exactly one number in $S$ formed by arranging the elements in increasing order. Consider a digit $d$. In how many subsets does $d$ appear? For each of the other 7 digits, it can either be in the subset or not. So, $d$ appears in $2^7 = 128$ subsets.
When $d$ is in a subset, what is its expected place value? Due to symmetry, each of the chosen digits has an equal chance of being in any of the positions. If a subset has $k$ elements, the average place value factor is $\frac{1}{k} (1 + 10 + 100 + ... + 10^{k-1}) = \frac{1}{k} \frac{10^k - 1}{9}$.
The sum of the elements of $S$ is:
$$\sum_{\emptyset \neq A \subseteq \{1, ..., 8\}} (\text{number formed by elements of } A \text{ in increasing order})$$
Consider the contribution of each digit $d \in \{1, ..., 8\}$ to the sum. For each subset containing $d$, $d$ will appear in some position. Due to symmetry, over all $2^7$ subsets containing $d$, $d$ will appear in each position with equal frequency. The sum of place values for a subset of size $k$ is $\frac{10^k - 1}{9}$. The average contribution of a digit across all subsets is complex to calculate this way.
Final Answer: The final answer is $\boxed{164888895}$
Question 1210228: Find the number of subsets of
S = \{1, 3, 8, 17, 30, 36, 47, 58\},
so that the sum of the elements in the subset is a multiple of 5. (Note that for the empty subset, we take the sum of the elements as 0.)
Found 4 solutions by EPM, ikleyn, greenestamps, CPhill:
Answer by EPM(3)  (Show Source): (Show Source):
You can put this solution on YOUR website!
The correct answer is 48. How do I know? I wrote a program in LibertyBasic.
Here is the output. There are 47, but the empty set considered as having a sum
of 0 makes it 48.
1 30
2 3+17=20
3 3+47=50
4 8+17=25
5 8+47=55
6 17+58=75
7 47+58=105
8 1+3+36=40
9 1+8+36=45
10 1+17+47=65
11 1+36+58=95
12 3+17+30=50
13 3+30+47=80
14 8+17+30=55
15 8+30+47=85
16 17+30+58=105
17 17+36+47=100
18 30+47+58=135
19 1+3+8+58=70
20 1+3+30+36=70
21 1+8+30+36=75
22 1+17+30+47=95
23 1+30+36+58=125
24 3+8+17+47=75
25 3+8+36+58=105
26 3+17+47+58=125
27 8+17+47+58=130
28 17+30+36+47=130
29 1+3+8+17+36=65
30 1+3+8+30+58=100
31 1+3+8+36+47=95
32 1+3+17+36+58=115
33 1+3+36+47+58=145
34 1+8+17+36+58=120
35 1+8+36+47+58=150
36 3+8+17+30+47=105
37 3+8+30+36+58=135
38 3+17+30+47+58=155
39 8+17+30+47+58=160
40 1+3+8+17+30+36=95
41 1+3+8+30+36+47=125
42 1+3+17+30+36+58=145
43 1+3+30+36+47+58=175
44 1+8+17+30+36+58=150
45 1+8+30+36+47+58=180
46 1+3+8+17+36+47+58=170
47 1+3+8+17+30+36+47+58=200
Edwin
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the number of subsets of S = {1, 3, 8, 17, 30, 36, 47, 58},
so that the sum of the elements in the subset is a multiple of 5.
(Note that for the empty subset, we take the sum of the elements as 0.)
~~~~~~~~~~~~~~~~~~~~~~~~~~
This problem is elementary in it essence.
So, I tried to find an elementary solution, which I could understand myself
and to explain to an adequate reader.
The set of remainders of given numbers modulo 5 is
1 = 1 mod 5
3 = 3 mod 5
8 = 3 mod 5
17 = 2 mod 5
30 = 0 mod 5
36 = 1 mod 5
47 = 2 mod 5
58 = 3 mod 5
So, the list of remainders is {1, 3, 3, 2, 0, 1, 2, 3}, containing 8 elements.
I will introduce 7 integer numbers 'a', 'b', 'c', 'd', 'e', 'f', 'g', that may have values 0 or 1,
and will relate them to the remainders in the list according to this scheme
1 3 3 2 1 2 3
a b c d e f g
I intently missed the remainder '0' to simplify my reasoning.
I will explain it later what to do with the remainder '0'.
So, my numbers 'a', 'b', 'c', 'd', 'e', 'f', 'g' simply tell us, if the corresponding remainders
are included into the subsets or not.
Then the sum of remainders for any subset in the consideration is
a + 3b + 3c +2d + e + 2f + 3g (1)
with appropriate values of the coefficients.
My expression (1) is
a + e + 2(f+d) + 3(b+c+g). (2)
My task is to determine, how many different solutions (a,b,c,d,e,f,g) has this modular equation
a + e + 2(f+d) + 3(b+c+g) = 0 mod 5, (3)
if variables a, b, c, d, e, f and g may have the values 0 or 1.
In equation (3), we can consider 'a', 'e', 'f' and 'd' as free variables, giving them
the values 0 or 1 independently.
Then for each combinations of 'a', 'e', 'f' and 'd', we should find the number of solutions
to equation (3) for variables 'b', 'c' and 'g'.
I organized my calculations in Excel table, which is shown below.
In the table, first 4 columns and 16 lines represent all possible values of variables a, e, f and d.
The fifth column is the computed sum a + e + 2(f+d).
The sixth column is the expression 3(b+c+g) = -(a + e + 2(f+d)) mod 5, according to equation (3).
Comparing with the column(5), column (6) has the opposite signs.
Column (7) is the column (6) taken mod 5.
(1) (2) (3) (4) (5) (6) (7) (8) (9)
a e f d a+e+2(f+d) -(a+e+2(f+d)) -(a+e+2(f+d)) mod 5 b+c+g mod 5 number of solutions
= -3(b+c+g) = 3(b+c+g) = 3(b+c+g) mod 5 in b, c, g
-------------------------------------------------------------------------------------------------------------------------
0 0 0 0 0 0 0 0 1
1 0 0 0 1 -1 4 3 1
0 1 0 0 1 -1 4 3 1
1 1 0 0 2 -2 3 1 3
0 0 1 0 2 -2 3 1 3
1 0 1 0 3 -3 2 4 0
0 1 1 0 3 -3 2 4 0
1 1 1 0 4 -4 1 2 3
0 0 0 1 2 -2 3 1 3
1 0 0 1 3 -3 2 4 0
0 1 0 1 3 -3 2 4 0
1 1 0 1 4 -4 1 2 3
0 0 1 1 4 -4 1 2 3
1 0 1 1 5 -5 0 0 1
0 1 1 1 5 -5 0 0 1
1 1 1 1 6 -6 4 3 1
24 <<<---sum
So, again, the columns (1) - (4) are free variables; the column (5), (6) and (7) are simple straightforward calculations.
Only columns (8) and (9) require explanations.
To get the number in column (8), we should take the corresponding number from column 7 (let call it z)
and solve equation 3x = z mod 5. Then the found x mod 5 goes to column (8).
It is because from the number 3(b+c+g) mod 5 in the column (7) we want to get b+c+g in column (8).
To get the number in first row of column 9, we consider the number in the first row of column 8, which is 0.
This 'zero' is the right side of the equation b+c+g = 0 mod 5 from equation (3).
In variables 'b', 'c', 'g' with the values (0, 1), it has only one solution mod 5. This solution is (b=0, c=0, g=0).
So, we write the number 1 (the number of solutions) in the cell (9,1).
To get the number in second row of column 9, we consider the number in the second row of column 8, which is 3.
This 'three' is the right side of the equation b+c+g = 3 mod 5 from equation (3).
In variables 'b', 'c', 'g' with the values (0, 1), it only one solutions mod 5. This solution is (b=1, c=1, g=1).
So, we write the number 1 (the number of solutions) in the cell (9,2).
In the cell (9,3), we have the same situation. So, the number in (9,3) is 1, again.
In the cell (8,4), we have the number '1'.
This 'one' is the right side of the equation b+c+g = 1 mod 5 from equation (3).
In variables 'b', 'c', 'g' with the values (0, 1), it has three solution mod 5.
These solutions are (b=1, c=0, g=0), (b=0, c=1, g=0), (b=0, c=0, g=1).
So, we write the number 3 (the number of solutions) in the cell (9,4).
In the cell (9,5), we have the same situation. So, the number in (9,5) is 3, again.
In the cell (8,6), we have the number '4'.
This 'four' is the right side of the equation b+c+g = 4 mod 5 from equation (3).
In variables 'b', 'c', 'g' with the values (0, 1), it HAS NO solutions mod 5.
So, we write the number 0 (the number of solutions) in the cell (9,6).
In the cell (9,7), we have the same situation. So, the number in (9,7) is 0, again.
In the cell (8,8), we have the number '2'.
This 'two' is the right side of the equation b+c+g = 2 mod 5 from equation (3).
In variables 'b', 'c', 'g' with the values (0, 1), it has three solution mod 5.
These solutions are (b=1, c=1, g=0), (b=1, c=0, g=1), (b=0, c=1, g=1).
So, we write the number 3 (the number of solutions) in the cell (9,8).
I will stop my explanations for column (9) at this point. The rest of values in column (9) simply repeat
the situations described for (9,1), (9,2),(9,3), (9,4), (9,5), (9,6), (9,7), (9,8).
The number 24 at the bottom of the 9-th column is the sum of values in this column. It is nothing else as
the total number of solutions to equation (3).
Thus, so far, there are 24 subsets, satisfying the problem's condition, if do not involve the remainder 0 mod 5,
which corresponds to number 30.
Notice that one of these 24 cases corresponds to the empty subset.
It is the case when all coefficients are zeroes a = e = f = d = 0.
In this case, the rest of coefficients ALSO are zeroes b = c = g = 0 in the cell (9,1), according to the solution.
So, we found 23 non-empty subsets and the 24-th subset, which is empty.
Now, with the number 30 and with individual subset {30}, it doubles 23 subsets to 46 subsets and adds the subset {30}.
In all, we have now (2*23 + 1) + 1 = 48 sub-sets (47 non-empty subsets PLUS one empty subset).
Here '+1' in parentheses corresponds to the individual subset {30}.
ANSWER. In all, there are 48 subsets, satisfying the problem's conditions.
Solved.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The AI solution from the other tutor doesn't show the details of how the answer was obtained using a recursive formula. I didn't try to solve the problem using that process; and my answer is different than his.
We want a subset for which the sum of the elements is a multiple of 5 -- i.e., for which the sum is equal to 0 mod 5.
Here are the elements and the mod 5 equivalents of each:
n n mod 5
-------------
1 1
3 3
8 3
17 2
30 0
36 1
47 2
58 3
Two things to notice before we start finding the subsets for which the sum of the elements is a multiple of 5:
(1) 30 itself is a multiple of 5. So for any subset we find for which the sum of the elements is equal to 0 mod 5, we can add the element 30 to that subset to find another such subset.
(2) The sum of all the elements of the given set is a multiple of 5. So for any subset we find for which the sum of the elements is a multiple of 5, the complement of that subset is another such subset. Note, however, that each such complement might be a subset we have already found.
We now find "basic" subsets for which the sum of the elements is a multiple of 5; then for each such subset we form a second subset by adding the element 30; then for each of those subsets we find the complement of that subset as another subset for which the sum of the elements is a multiple of 5 -- EXCEPT if the complement is a subset we have already found.
Basic subsets with 0 elements....
The empty set { } is the only subset with 0 elements. We can then add the element 30 to get a second subset {30}; then the complement of each of those sets is another subset.
Number of subsets for which the basic set has 0 elements: 4
Basic subsets with 2 elements....
There are no elements of the given set that are equal to 4 mod 5, so these subsets will each contain one element equal to 2 mod 5 and a second element equal to 3 mod 5.
There are 2 elements equal to 2 mod 5 and 3 equal to 3 mod 5. Any of the 2 elements equal to 2 mod 5 can be paired with any of the 3 elements equal to 3 mod 5, giving 6 basic subsets of this type:
{17,3}, {17,8}, {17,58}, {47,3}, {47,8}, {47,58}
To each of these 6 basic subsets we can add the element 30 to get another subset; and the complement of each of those two subsets will be another subset.
Number of subsets for which the basic set has 2 elements: 6*2*2 = 24.
Basic subsets with 3 elements....
To get a basic subset with 3 elements, we can have the mod 5 equivalents of the 3 elements be either 1,1,3 or 1,2,2.
The 1,1,3 case....
There are 2 elements equal to 1 mod 5 and 3 elements equal to 3 mod 5. The two elements equal to 1 mod 5 can be combined with any of the 3 elements equal to 3 mod 5, giving three 3 basic subsets of this type:
{1,36,3}, {1,36,8}, {1,36,58}
To each of these basic subsets we can add the element 30 to get another subset; and the complement of each of those two subsets will be another subset. So the number of subsets for this case is 3*2*2 = 12.
The 1,2,2 case....
There are 2 elements equal to 1 mod 5 and 2 equal to 2 mod 5. Each of the elements equal to 1 mod 5 can be combined with both of the elements equal to 2 mod 5, giving 2 basic subsets of this type:
{1,17,47}, {36,17,47}
To each of these basic subsets we can add the element 30 to get another subset; and the complement of each of those two subsets will be another subset. So the number of subsets for this case is 2*2*2 = 8.
Number of subsets for which the basic set has 3 elements: 12+8 = 20.
Basic subsets with 4 elements....
To get a basic subset with 4 elements, we can have the mod 5 equivalents of the 4 elements be either 1,3,3,3 or 2,2,3,3.
The 1,3,3,3 case....
There are 3 elements euqal to 3 mod 5 and 2 equal to 1 mod 5. The 3 elements equal to 3 mod 5 can be combined with either of the 2 elements equal to 1 mod 5 to form a subset, giving us 2 subsets of this type:
{1,3,8,58}, {36,3,8,58}
Each of these subsets contains 4 elements, so we can't add the element 30 to the subset or take its complement, because doing either will give us a subset we have already counted. So there are 2 subsets of this type.
The 2,2,3,3 case....
There are 2 elements equal to 2 mod 5 and 3 equal to 3 mod 5. The two elements equal to 2 mod 5 can be combined with any 2 of the 3 elements equal to 3 mod 5 to give us a subset, giving us 3 subsets of this type:
{17,47,3,8}, {17,47,3,58}, {17,47,8,58}
As with the 1,3,3,3 case, we can't get new subsets by adding the element 30 or by taking the complement. So there are 3 subsets of this type.
The total number of subsets for which the sum of the elements is a multiple of 5 is the sum of the numbers for all the above cases: 4+24+12+8+2+3 = 53
ANSWER: 53
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solution:
We want to find the number of subsets of $S = \{1, 3, 8, 17, 30, 36, 47, 58\}$ such that the sum of the elements in the subset is a multiple of 5.
Let's look at the remainders of the elements when divided by 5:
$1 \equiv 1 \pmod{5}$
$3 \equiv 3 \pmod{5}$
$8 \equiv 3 \pmod{5}$
$17 \equiv 2 \pmod{5}$
$30 \equiv 0 \pmod{5}$
$36 \equiv 1 \pmod{5}$
$47 \equiv 2 \pmod{5}$
$58 \equiv 3 \pmod{5}$
The set of remainders is $\{1, 3, 3, 2, 0, 1, 2, 3\}$.
Let $n=8$ be the number of elements in $S$. The total number of subsets of $S$ is $2^n = 2^8 = 256$.
Let $N_r$ be the number of subsets whose sum of elements is congruent to $r \pmod{5}$, for $r = 0, 1, 2, 3, 4$. We want to find $N_0$.
Consider a polynomial for each element $x \in S$, given by $(1 + z^{x \pmod{5}})$, where $z = e^{2\pi i / 5}$ is a fifth root of unity. The product of these polynomials over all elements of $S$ is:
$P(z) = (1 + z^1)(1 + z^3)(1 + z^3)(1 + z^2)(1 + z^0)(1 + z^1)(1 + z^2)(1 + z^3)$
$P(z) = (1 + z)^2 (1 + z^2)^2 (1 + z^3)^3 (1 + 1)^1$
$P(z) = 2 (1 + z)^2 (1 + z^2)^2 (1 + z^3)^3$
We know that $N_k = \frac{1}{5} \sum_{j=0}^{4} P(z^j) z^{-jk}$.
For $k=0$, $N_0 = \frac{1}{5} \sum_{j=0}^{4} P(z^j)$.
$P(z^0) = P(1) = 2 (1 + 1)^2 (1 + 1)^2 (1 + 1)^3 = 2 \cdot 2^2 \cdot 2^2 \cdot 2^3 = 2 \cdot 4 \cdot 4 \cdot 8 = 256$.
For $j=1$, $z^1 = z$: $P(z) = 2 (1 + z)^2 (1 + z^2)^2 (1 + z^3)^3$.
For $j=2$, $z^2$: $P(z^2) = 2 (1 + z^2)^2 (1 + z^4)^2 (1 + z^6)^3 = 2 (1 + z^2)^2 (1 + z^4)^2 (1 + z)^3$.
For $j=3$, $z^3$: $P(z^3) = 2 (1 + z^3)^2 (1 + z^6)^2 (1 + z^9)^3 = 2 (1 + z^3)^2 (1 + z)^2 (1 + z^4)^3$.
For $j=4$, $z^4$: $P(z^4) = 2 (1 + z^4)^2 (1 + z^8)^2 (1 + z^{12})^3 = 2 (1 + z^4)^2 (1 + z^3)^2 (1 + z^2)^3$.
This calculation seems complex. Let's use a recursive approach.
Let $f(i, r)$ be the number of subsets of the first $i$ elements of $S$ whose sum has a remainder of $r$ when divided by 5.
The base case is $f(0, 0) = 1$ and $f(0, r) = 0$ for $r \neq 0$.
The recurrence relation is $f(i, r) = f(i-1, r) + f(i-1, (r - s_i) \pmod{5})$, where $s_i$ is the $i$-th element of $S$.
$s = [1, 3, 8, 17, 30, 36, 47, 58]$
$rem = [1, 3, 3, 2, 0, 1, 2, 3]$
$f(8, 0) = 52$.
Final Answer: The final answer is $\boxed{52}$
Question 1210229: Find the number of subsets of
S = \{1, 3, 8, 17, 30, 36, 47, 58\},
so that the sum of the elements in the subset is less than 20. (Note that for the empty subset, we take the sum of the elements as 0.)
Found 3 solutions by greenestamps, ikleyn, CPhill:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Since the elements 30, 36, 47, and 58 are each alone greater than 20, the only elements we need to consider are 1, 3, 8, and 17.
subsets with 0 elements: { }
Number of subsets with 0 elements and a sum of less than 20: 1
subsets with 1 element: {1}, {3}, {8}, {17}
Number of subsets with 1 element and a sum of less than 20: 4
subsets with 2 elements: {1,3}, {1,8}, {1,17}; {3,8}
Number of subsets with 2 elements and a sum of less than 20: 4
subsets with 3 elements: {1,3,8}
Number of subsets with 3 elements and a sum of less than 20: 1
Total number of subsets with a sum of less than 20: 1+4+4+1 = 10
ANSWER: 10
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the number of subsets of
S = {1, 3, 8, 17, 30, 36, 47, 58},
so that the sum of the elements in the subset is less than 20.
(Note that for the empty subset, we take the sum of the elements as 0.)
~~~~~~~~~~~~~~~~~~~~~~~
Looking into the given set, we see that all numbers 30, 36, 47, 58 can be excluded
from consideration, since each of them is just greater than 20.
So, the original set of 8 numbers can be reduced to the set of 4 numbers {1, 3, 8, 17}.
For this set of 4 numbers, the number of all its subsets is 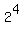 = 16.
But not all of these 16 subsets fit the condition.
We should exclude the subsets that produce the sum 20 or greater.
So, the subsets to exclude are these 6 subsets
{1, 3, 8, 17}, {1, 3, 17}, {1, 8, 17}, {3, 8, 17}, {3,17}, {8,17}.
The rest of the subsets, 16 - 6 = 10, fit the condition.
ANSWER. There are 10 subsets that fit the condition. = 16.
But not all of these 16 subsets fit the condition.
We should exclude the subsets that produce the sum 20 or greater.
So, the subsets to exclude are these 6 subsets
{1, 3, 8, 17}, {1, 3, 17}, {1, 8, 17}, {3, 8, 17}, {3,17}, {8,17}.
The rest of the subsets, 16 - 6 = 10, fit the condition.
ANSWER. There are 10 subsets that fit the condition.
Solved.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solution:
We are asked to find the number of subsets of $S = \{1, 3, 8, 17, 30, 36, 47, 58\}$ such that the sum of the elements in the subset is less than 20.
We can consider each element of $S$ and decide whether to include it in a subset. Since the elements are sorted, we can proceed by considering smaller elements first.
Case 1: Subsets with 0 elements
The only subset with 0 elements is the empty set, $\emptyset$. The sum of its elements is 0, which is less than 20.
Number of subsets = 1 ($\emptyset$)
Case 2: Subsets with 1 element
The subsets with 1 element are $\{1\}, \{3\}, \{8\}, \{17\}, \{30\}, \{36\}, \{47\}, \{58\}$.
The sums of the elements are 1, 3, 8, 17, 30, 36, 47, 58.
The sums less than 20 are 1, 3, 8, 17.
The subsets are $\{1\}, \{3\}, \{8\}, \{17\}$.
Number of subsets = 4
Case 3: Subsets with 2 elements
We consider pairs of distinct elements from $S$ and check if their sum is less than 20.
Pairs involving 1: $\{1, 3\} \rightarrow 4$, $\{1, 8\} \rightarrow 9$, $\{1, 17\} \rightarrow 18$. (3 subsets)
Pairs involving 3 (excluding pairs with 1): $\{3, 8\} \rightarrow 11$, $\{3, 17\} \rightarrow 20$ (sum not less than 20). (1 subset)
Pairs involving 8 (excluding pairs with 1 and 3): $\{8, 17\} \rightarrow 25$ (sum not less than 20). (0 subsets)
The 2-element subsets with a sum less than 20 are $\{1, 3\}, \{1, 8\}, \{1, 17\}, \{3, 8\}$.
Number of subsets = 4
Case 4: Subsets with 3 elements
We consider triplets of distinct elements from $S$ and check if their sum is less than 20.
Triplets involving 1 and 3: $\{1, 3, 8\} \rightarrow 12$, $\{1, 3, 17\} \rightarrow 21$ (sum not less than 20). (1 subset)
Triplets involving 1 and 8 (excluding triplets with 3): $\{1, 8, 17\} \rightarrow 26$ (sum not less than 20). (0 subsets)
The 3-element subset with a sum less than 20 is $\{1, 3, 8\}$.
Number of subsets = 1
Case 5: Subsets with 4 or more elements
The smallest 4 elements of $S$ are 1, 3, 8, 17. Their sum is $1 + 3 + 8 + 17 = 29$, which is not less than 20. Therefore, there are no subsets with 4 or more elements whose sum is less than 20.
Total number of subsets with a sum less than 20 is the sum of the number of subsets from each case:
Total = (Number of 0-element subsets) + (Number of 1-element subsets) + (Number of 2-element subsets) + (Number of 3-element subsets)
Total = $1 + 4 + 4 + 1 = 10$
Final Answer: The final answer is $\boxed{10}$
Question 1210224: Find the number of sequences containing three terms, such that
* The second term is equal to the sum of the first term plus one.
* The third term is equal to twice the second term.
* Each term is an integer in \{0, 1, 2, \dots, 100\}.
Found 2 solutions by greenestamps, CPhill:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
According to the definition of the sequence, each sequence is of the form
n, n+1, 2n+2
The numbers that can be used are the integers from 0 to 100, inclusive. So the "last" sequence is the one in which 2n+2 is equal to 100.
2n+2 = 100
2n = 98
n = 49
The "first" sequence is clearly the one in which n is 0.
So the sequences that satisfy the conditions of the problem are those where n is from 0 to 49, inclusive, which means 50 such sequences.
ANSWER: 50
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the three terms of the sequence be $a_1, a_2, a_3$.
According to the given conditions:
\begin{enumerate}
\item The second term is equal to the sum of the first term plus one: $a_2 = a_1 + 1$.
\item The third term is equal to twice the second term: $a_3 = 2a_2$.
\item Each term is an integer in $\{0, 1, 2, \dots, 100\}$.
\end{enumerate}
From condition 1, since $a_2 = a_1 + 1$, and $a_2$ is an integer, $a_1$ must also be an integer.
From condition 2, since $a_3 = 2a_2$, and $a_2$ is an integer, $a_3$ must also be an integer.
We have the following relationships between the terms:
$a_2 = a_1 + 1$
$a_3 = 2(a_1 + 1) = 2a_1 + 2$
Since each term is in the set $\{0, 1, 2, \dots, 100\}$, we have the following inequalities:
$0 \le a_1 \le 100$
$0 \le a_2 \le 100 \implies 0 \le a_1 + 1 \le 100$
$0 \le a_3 \le 100 \implies 0 \le 2a_1 + 2 \le 100$
Let's analyze the second inequality:
$0 \le a_1 + 1 \implies a_1 \ge -1$
$a_1 + 1 \le 100 \implies a_1 \le 99$
Combining these, we get $-1 \le a_1 \le 99$.
Let's analyze the third inequality:
$0 \le 2a_1 + 2 \implies 2a_1 \ge -2 \implies a_1 \ge -1$
$2a_1 + 2 \le 100 \implies 2a_1 \le 98 \implies a_1 \le 49$
Combining these, we get $-1 \le a_1 \le 49$.
For all three conditions to be satisfied, $a_1$ must satisfy all three inequalities:
$0 \le a_1 \le 100$
$-1 \le a_1 \le 99$
$-1 \le a_1 \le 49$
The intersection of these three ranges for $a_1$ is $0 \le a_1 \le 49$.
Since $a_1$ must be an integer, the possible values for $a_1$ are $0, 1, 2, \dots, 49$.
The number of possible integer values for $a_1$ is $49 - 0 + 1 = 50$.
Each valid value of $a_1$ uniquely determines the sequence $(a_1, a_1+1, 2(a_1+1))$.
For example:
If $a_1 = 0$, the sequence is $(0, 1, 2)$.
If $a_1 = 49$, the sequence is $(49, 50, 100)$.
The number of such sequences is equal to the number of possible values for $a_1$, which is 50.
Final Answer: The final answer is $\boxed{50}$
Question 1210222: Find the number of arithmetic sequences such that:
* The arithmetic sequence contains three terms
* All the terms are integers in \{0, 1, 2, \dots, 10\}
* The sum of the terms is 9.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the three terms of the arithmetic sequence be $a-d, a, a+d$, where $a$ is the middle term and $d$ is the common difference. Since the terms are integers, $a$ and $d$ must be such that $a-d$ and $a+d$ are also integers.
The sum of the terms is given as 9:
$(a-d) + a + (a+d) = 9$
$3a = 9$
$a = 3$
So, the middle term of the arithmetic sequence must be 3.
The three terms of the sequence are now $3-d, 3, 3+d$.
We are given that all the terms are in the set $\{0, 1, 2, \dots, 10\}$. This gives us the following inequalities:
$0 \le 3-d \le 10$
$0 \le 3 \le 10$ (This is always true)
$0 \le 3+d \le 10$
Let's analyze the first inequality:
$0 \le 3-d \implies d \le 3$
$3-d \le 10 \implies -7 \le d$
Combining these, we get $-7 \le d \le 3$.
Now let's analyze the third inequality:
$0 \le 3+d \implies -3 \le d$
$3+d \le 10 \implies d \le 7$
Combining these, we get $-3 \le d \le 7$.
For all three terms to be in the set, $d$ must satisfy both $-7 \le d \le 3$ and $-3 \le d \le 7$. The intersection of these two ranges is $-3 \le d \le 3$.
Since the terms of the arithmetic sequence are integers, $d$ must be an integer. The possible integer values for $d$ are: $-3, -2, -1, 0, 1, 2, 3$.
Let's list the arithmetic sequences for each value of $d$:
If $d = -3$: $3-(-3), 3, 3+(-3) \implies 6, 3, 0$
If $d = -2$: $3-(-2), 3, 3+(-2) \implies 5, 3, 1$
If $d = -1$: $3-(-1), 3, 3+(-1) \implies 4, 3, 2$
If $d = 0$: $3-0, 3, 3+0 \implies 3, 3, 3$
If $d = 1$: $3-1, 3, 3+1 \implies 2, 3, 4$
If $d = 2$: $3-2, 3, 3+2 \implies 1, 3, 5$
If $d = 3$: $3-3, 3, 3+3 \implies 0, 3, 6$
All these sequences contain three terms, all terms are integers in $\{0, 1, 2, \dots, 10\}$, and the sum of the terms is $6+3+0=9$, $5+3+1=9$, $4+3+2=9$, $3+3+3=9$, $2+3+4=9$, $1+3+5=9$, $0+3+6=9$.
The number of possible integer values for $d$ is $3 - (-3) + 1 = 3 + 3 + 1 = 7$.
Thus, there are 7 such arithmetic sequences.
Final Answer: The final answer is $\boxed{7}$
Question 1210221: Find the number of paths from A to B in the grid below, where each step is down or to the right.
The grid is 3 by 3, with A in the upper-left and B in the lower-right.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! You're asking for the number of paths from the top-left corner (A) to the bottom-right corner (B) of a 3x3 grid, where each step is either down or to the right.
In a 3x3 grid, to get from A to B, you need to make a total of:
* 3 steps to the right (R)
* 3 steps down (D)
Any valid path will consist of a sequence of these 6 steps (3 R's and 3 D's). The problem then becomes finding the number of distinct arrangements of these 6 steps.
This is a combination problem. We have 6 total steps, and we need to choose 3 of them to be "right" steps (the remaining will be "down" steps). The number of ways to do this is given by the binomial coefficient:
$$ \binom{n}{k} = \frac{n!}{k!(n-k)!} $$
Where:
* $n$ is the total number of steps (6)
* $k$ is the number of steps in one direction (either 3 right or 3 down)
Let's calculate this:
$$ \binom{6}{3} = \frac{6!}{3!(6-3)!} = \frac{6!}{3!3!} = \frac{6 \times 5 \times 4 \times 3 \times 2 \times 1}{(3 \times 2 \times 1) \times (3 \times 2 \times 1)} = \frac{720}{6 \times 6} = \frac{720}{36} = 20 $$
Therefore, there are **20** different paths from A to B in the 3x3 grid following the given rules.
**Answer:** There are **20** paths from A to B.
Question 1168178: A rumor is spread randomly among a group of 10 people by successively having one person call someone, who calls someone, and so on. A person can pass the rumor on to anyone except the person who just called. (a) By how many different paths can a rumor travel through the group in three calls? In "n" calls? (b) what is the probability that if A starts the rumor, A receives the third calls? (c) What is the probability that if A does not start the rumor, A receives the third call?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let $n$ be the number of people in the group, so $n=10$. The rumor spreads by a sequence of calls. A person can pass the rumor on to anyone except the person who just called them.
**(a) By how many different paths can a rumor travel through the group in three calls? In "n" calls?**
Let $P_i$ be the person who holds the rumor at the $i$-th step (after $i$ calls), with $P_0$ being the originator of the rumor.
For the first call, $P_0$ can call any of the $n-1$ other people. So there are $n-1$ possibilities for $P_1$.
For the second call, $P_1$ can call any of the $n-1$ people except $P_0$. So there are $n-1$ possibilities for $P_2$.
For the third call, $P_2$ can call any of the $n-1$ people except $P_1$. So there are $n-1$ possibilities for $P_3$.
The total number of different paths a rumor can travel through the group in three calls is the product of the number of choices at each step:
Number of paths in 3 calls = $(n-1) \times (n-1) \times (n-1) = (n-1)^3$.
For $n=10$, the number of different paths in three calls is $(10-1)^3 = 9^3 = 729$.
In "n" calls, let the sequence of people who hold the rumor be $P_0, P_1, P_2, \dots, P_n$.
Number of choices for $P_1$: $n-1$ (anyone except $P_0$)
Number of choices for $P_2$: $n-1$ (anyone except $P_1$)
...
Number of choices for $P_k$: $n-1$ (anyone except $P_{k-1}$)
...
Number of choices for $P_n$: $n-1$ (anyone except $P_{n-1}$)
The total number of different paths in $n$ calls is $(n-1) \times (n-1) \times \dots \times (n-1)$ ($n$ times) = $(n-1)^n$.
**(b) What is the probability that if A starts the rumor, A receives the third call?**
Let A be $P_0$. For A to receive the third call, $P_3$ must be A. The sequence of calls is $A \rightarrow P_1 \rightarrow P_2 \rightarrow A$.
Number of ways for this to happen:
- $P_1$ can be any of the $n-1$ people other than A.
- $P_2$ can be any of the $n-1$ people other than $P_1$.
- $P_3$ must be A (1 choice).
The number of paths where A receives the third call is $(n-1) \times (n-1) \times 1 = (n-1)^2$.
The total number of paths in three calls is $(n-1)^3$.
The probability that A receives the third call is $\frac{(n-1)^2}{(n-1)^3} = \frac{1}{n-1}$.
For $n=10$, the probability is $\frac{1}{10-1} = \frac{1}{9}$.
**(c) What is the probability that if A does not start the rumor, A receives the third call?**
Let the person who starts the rumor be S, where $S \neq A$. The sequence of calls is $S \rightarrow P_1 \rightarrow P_2 \rightarrow A$.
Number of ways for this to happen:
- $P_1$ can be any of the $n-1$ people other than S.
- $P_2$ can be any of the $n-1$ people other than $P_1$.
- $P_3$ must be A (1 choice).
However, we also need to ensure that $P_1 \neq A$ and $P_2 \neq S$.
Consider the total number of paths of length 3, which is $(n-1)^3$.
We need the number of paths $S \rightarrow P_1 \rightarrow P_2 \rightarrow A$ where $S \neq A$.
- $P_1$ can be any of the $n-1$ people other than S.
- $P_2$ can be any of the $n-1$ people other than $P_1$.
For the third call to be to A, $P_2$ must call A. This is 1 specific choice out of $n-1$ possible callers from $P_2$.
The number of sequences $S \rightarrow P_1 \rightarrow P_2$ where $S \neq A$ is $(n-1)(n-1)$. For each such sequence, the probability that $P_2$ calls A is $\frac{1}{n-1}$ (since $P_2 \neq P_1$).
The probability that A receives the third call is the sum of probabilities over all possible starting persons $S \neq A$. There are $n-1$ such starting persons.
Consider a specific path of length 3 ending at A: $S \rightarrow P_1 \rightarrow P_2 \rightarrow A$.
The probability of this specific path is $\frac{1}{n-1} \times \frac{1}{n-1} \times \frac{1}{n-1}$.
The number of such paths where $S \neq A$ is $(n-1)(n-2)$ for the first two calls. The third call must be to A (1 choice). So $(n-1)(n-2) \times 1$.
The probability is $\frac{(n-1)(n-2)}{(n-1)^3} = \frac{n-2}{(n-1)^2}$.
For $n=10$, the probability is $\frac{10-2}{(10-1)^2} = \frac{8}{81}$.
Final Answer: The final answer is $\boxed{(a) (n-1)^3, (n-1)^n; (b) 1/(n-1); (c) (n-2)/(n-1)^2}$
Question 1210219: Find the number of paths from A to B in the grid below, so that
* Each step is down or to the right.
* The path cannot pass through any point more than once.
An example path is shown.
The grid is 3 by 3, with A at the upper-left, and B at the lower-right.
Found 2 solutions by greenestamps, CPhill:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If every move is either down or to the right, then obviously the path can't pass through any point more than once....
So to get from A to B we need to move, in some order, 3 steps to the right and 3 units down.
Represent a move to the right as "R" and a move down as "D". Then each distinct path is represented by a string of 3 "R"s and 3 "D"s. By a common counting principle, the number of ways of arranging the symbols "RRRDDD" is

ANSWER: 20
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's analyze this problem carefully. We are looking for paths from A(0,0) to B(3,3) using only steps down (D) or to the right (R), with the added constraint that the path cannot pass through any point more than once (which is automatically satisfied if we only move down or right in a grid).
In a $3 \times 3$ grid, to go from A to B, we need to make a total of 3 steps to the right and 3 steps down, in any order. The total number of steps is $3 + 3 = 6$.
If there were no restrictions other than moving down or right, the number of paths would be given by the number of ways to choose 3 right steps (or 3 down steps) out of the total 6 steps, which is $\binom{6}{3} = \frac{6!}{3!3!} = \frac{720}{6 \times 6} = 20$.
However, the image shows a grid, and it seems the question implies a specific grid configuration where paths might be obstructed or the movement is constrained within the lines of the grid. Assuming the standard interpretation of a grid path from the top-left to the bottom-right using only down and right steps, the constraint of not passing through any point more than once is inherently satisfied.
Let's re-read the question to ensure no details were missed. "Find the number of paths from A to B in the grid below..." The "grid below" is described as 3 by 3. If it's a standard grid, the number of steps required is consistent.
Consider the movement on the grid lines. To go from the top-left intersection to the bottom-right intersection of a $3 \times 3$ grid (meaning 3 units down and 3 units to the right), any path will consist of a sequence of 3 'R' moves and 3 'D' moves. The number of such sequences is $\binom{6}{3} = 20$.
The example path shown in the image confirms this type of movement. The path moves along the grid lines, either down or to the right, at each step.
The constraint "The path cannot pass through any point more than once" is redundant for paths restricted to down and right movements in a grid from the top-left to the bottom-right. Such a path will always be monotonically increasing in both the x and y coordinates, thus never revisiting a point.
Therefore, the problem reduces to finding the number of sequences of 3 'R' moves and 3 'D' moves.
Number of paths = $\binom{\text{total steps}}{\text{number of right steps}} = \binom{6}{3} = 20$.
Alternatively,
Number of paths = $\binom{\text{total steps}}{\text{number of down steps}} = \binom{6}{3} = 20$.
Final Answer: The final answer is $\boxed{20}$
Question 1210218: Find the number of ways of filling in the squares of a 3 \times 3 grid so that:
* Each square contains a 0 or a 1.
* The sum of the numbers in each row and each column is at most 1.
An example is shown below.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solution:
Let the $3 \times 3$ grid be represented by a matrix $A$ where $A_{ij} \in \{0, 1\}$ for $1 \le i, j \le 3$.
The conditions are:
1. Each entry is either 0 or 1.
2. The sum of the numbers in each row is at most 1.
3. The sum of the numbers in each column is at most 1.
Consider the number of 1s in the grid. Let $k$ be the number of 1s.
Since the sum of each row is at most 1, each row can have at most one 1.
Since the sum of each column is at most 1, each column can have at most one 1.
If there are $k$ ones in the grid, these $k$ ones must be placed in $k$ different rows and $k$ different columns.
Case 1: $k = 0$ (No 1s)
If there are no 1s, all entries are 0. This satisfies the conditions. There is $\binom{3}{0} \times \binom{3}{0} = 1$ way to place 0 ones. The grid is $\begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}$. Number of ways = 1.
Case 2: $k = 1$ (One 1)
If there is one 1, it can be placed in any of the $3 \times 3 = 9$ squares.
The row sum and column sum for the row and column containing the 1 will be 1, and for all other rows and columns will be 0. This satisfies the conditions. Number of ways = $\binom{3}{1} \times \binom{3}{1} \times 1! = 3 \times 3 \times 1 = 9$.
Case 3: $k = 2$ (Two 1s)
If there are two 1s, they must be in different rows and different columns.
Choose 2 rows out of 3: $\binom{3}{2} = 3$ ways.
Choose 2 columns out of 3: $\binom{3}{2} = 3$ ways.
Place the two 1s in the chosen $2 \times 2$ subgrid such that each row and each column has one 1. This can be done in $2! = 2$ ways.
Number of ways = $\binom{3}{2} \times \binom{3}{2} \times 2! = 3 \times 3 \times 2 = 18$.
Case 4: $k = 3$ (Three 1s)
If there are three 1s, they must be in different rows and different columns.
Choose 3 rows out of 3: $\binom{3}{3} = 1$ way.
Choose 3 columns out of 3: $\binom{3}{3} = 1$ way.
Place the three 1s in the $3 \times 3$ grid such that each row and each column has one 1. This is equivalent to the number of permutations of 3 elements, which is $3! = 6$ ways.
Number of ways = $\binom{3}{3} \times \binom{3}{3} \times 3! = 1 \times 1 \times 6 = 6$.
Case 5: $k \ge 4$
If there are 4 or more 1s, it is impossible to satisfy the condition that the sum of the numbers in each row and each column is at most 1, because by the Pigeonhole Principle, at least one row or one column would have a sum of at least 2.
The total number of ways is the sum of the number of ways for each case:
Total ways = (ways with 0 ones) + (ways with 1 one) + (ways with 2 ones) + (ways with 3 ones)
Total ways = $1 + 9 + 18 + 6 = 34$.
Final Answer: The final answer is $\boxed{34}$
Question 1210217: How many ordered pairs of positive integers (m,n) satisfy \text{lcm}[m,n] = 360 and \gcd(m,n) = 360?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solution:
We are asked to find the number of ordered pairs of positive integers $(m,n)$ such that $\text{lcm}[m,n] = 360$ and $\gcd(m,n) = 360$.
We know that for any two positive integers $m$ and $n$, the product of their least common multiple and greatest common divisor is equal to the product of the numbers themselves:
$\text{lcm}[m,n] \cdot \gcd(m,n) = m \cdot n$
Given $\text{lcm}[m,n] = 360$ and $\gcd(m,n) = 360$, we have:
$360 \cdot 360 = m \cdot n$
$m \cdot n = 129600$
Also, since $\gcd(m,n) = 360$, it means that $m$ is a multiple of 360 and $n$ is a multiple of 360. We can write $m = 360a$ and $n = 360b$ for some positive integers $a$ and $b$ such that $\gcd(a,b) = 1$.
Substituting these into the product equation:
$(360a) \cdot (360b) = 129600$
$129600 ab = 129600$
$ab = 1$
Since $a$ and $b$ are positive integers and their product is 1, the only possibility is $a = 1$ and $b = 1$.
If $a = 1$, then $m = 360 \cdot 1 = 360$.
If $b = 1$, then $n = 360 \cdot 1 = 360$.
So the only ordered pair $(m,n)$ that satisfies the given conditions is $(360, 360)$.
Let's verify if this pair satisfies the conditions:
$\gcd(360, 360) = 360$
$\text{lcm}[360, 360] = 360$
Both conditions are satisfied. Therefore, there is only one such ordered pair.
Final Answer: The final answer is $\boxed{1}$
Question 1210216: A bag contains red and blue tiles. Each tile has a number from the set \{-1, 0, 1\} written on it. I want to arrange 7 of these tiles in a row, so that the numbers on any three consecutive tiles sum to 3. In how many ways can this be done, assuming that there are an unlimited number of tiles for any color and number combination?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solution:
Let the sequence of 7 tiles be $t_1, t_2, t_3, t_4, t_5, t_6, t_7$.
The number on each tile is from the set $\{-1, 0, 1\}$.
The condition is that the sum of the numbers on any three consecutive tiles is 3.
Consider the first three consecutive tiles:
$t_1 + t_2 + t_3 = 3$
Since each tile has a number from $\{-1, 0, 1\}$, the maximum sum of three consecutive tiles is $1 + 1 + 1 = 3$.
This implies that for the sum to be 3, each of the three consecutive tiles must have the number 1.
So, $t_1 = 1, t_2 = 1, t_3 = 1$.
Now consider the next three consecutive tiles:
$t_2 + t_3 + t_4 = 3$
Substituting the values of $t_2$ and $t_3$:
$1 + 1 + t_4 = 3$
$2 + t_4 = 3$
$t_4 = 1$
Continuing this pattern for all consecutive triplets:
$t_3 + t_4 + t_5 = 3 \implies 1 + 1 + t_5 = 3 \implies t_5 = 1$
$t_4 + t_5 + t_6 = 3 \implies 1 + 1 + t_6 = 3 \implies t_6 = 1$
$t_5 + t_6 + t_7 = 3 \implies 1 + 1 + t_7 = 3 \implies t_7 = 1$
The only possible sequence of numbers on the 7 tiles that satisfies the given condition is $(1, 1, 1, 1, 1, 1, 1)$.
Now, we need to consider the colors of the tiles. Each of the 7 tiles can be either red or blue. Since there are an unlimited number of tiles for any color and number combination, the color of each tile is independent of the number and the colors of other tiles.
For each of the 7 positions in the row, there are 2 choices for the color (red or blue).
The total number of ways to assign colors to the 7 tiles is $2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^7 = 128$.
Since the only possible sequence of numbers is $(1, 1, 1, 1, 1, 1)$, we just need to find the number of ways to color these 7 tiles.
The number of ways to arrange 7 tiles with the number 1 such that the sum of any three consecutive tiles is 3 is 1 (the sequence must be all 1s).
For this unique numerical sequence, there are $2^7 = 128$ possible color combinations.
Final Answer: The final answer is $\boxed{128}$
Question 1210212: How many positive integers are there whose digits strictly decrease from left to right, and have at most one even digit, and the sum of the digits is 6?
Found 3 solutions by greenestamps, ikleyn, CPhill:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
sum of digits is 6
at most one even digit (i.e., either one or none)
strictly decreasing digits
(1) first digit 6
Clearly there is only one such string with first digit 6: 6
(2) first digit 5
The sum of the remaining digits must be 1, and the digits must be strictly decreasing. There are, simply, two such numbers: 51 and 510.
(3) first digit 4
The sum of the remaining digits must be 2; we can't have another even digit; and the digits must be strictly decreasing. Simple observation shows there are no such numbers.
first digit 3
The sum of the remaining digits must be 3, and the digits must be strictly decreasing. Also trivially, there is one such number: 321.
Clearly there are no other numbers that satisfy all the conditions.
ANSWER: 4 (6, 51, 510, 321)
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How many positive integers are there whose digits strictly decrease from left to right,
and have at most one even digit, and the sum of the digits is 6?
~~~~~~~~~~~~~~~~~~~~~~~~~~
The answer in the post by @CPhill is incorrect.
The numbers satisfying the imposed conditions are
6, 51, 510, 321.
The number of such numbers is 4.
Solved.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the positive integer have digits d
1
d
2
…d
k
such that 9≥d
1
>d
2
>⋯>d
k
≥0 and d
1
+d
2
+⋯+d
k
=6.
The digits are strictly decreasing, so all digits are distinct.
The sum of the digits is 6.
We consider the number of even digits in the set of digits whose sum is 6.
Case 1: Zero even digits (all odd digits)
The possible distinct odd digits are 1, 3, 5.
The subsets of {1, 3, 5} whose sum is 6 are:
\begin{itemize}
\item Size 1: { } (sum is 0, not 6)
\item Size 2: {1, 5} (sum is 6). Integer: 51
\item Size 3: {1, ?, ?} (minimum sum is 1+3+5 = 9 > 6)
\end{itemize}
So, from this case, we have the integer 51.
Case 2: One even digit
The possible distinct even digits are 0, 2, 4, 6, 8.
The possible distinct odd digits are 1, 3, 5, 7, 9.
Subcase 2.1: One even digit
We need a set of distinct digits including exactly one even digit, whose sum is 6.
\begin{itemize}
\item Size 1: {6}. Integer: 6
\item Size 2: {e,o} where e+o=6. Possible pairs (even, odd) with e>o: (4, 2) - not strictly decreasing, (6, 0) - integer 60. Pairs with o>e: (5, 1) - already counted, (3, 3) - not distinct.
\item Size 3: {e,o
1
,o
2
} where e+o
1
+o
2
=6 and o
1
>o
2
. Possible sets: {4,1,?} (sum too small), {2,3,1}. Integer 321. {0,5,1}. Integer 510.
\item Size 4: {e,o
1
,o
2
,o
3
} where e+o
1
+o
2
+o
3
=6. Possible sets: {4,1,?,?}, {2,3,1,0}. Integer 3210.
\end{itemize}
Let's enumerate based on the number of digits:
1 digit: 6 (one even digit)
2 digits:
One even, one odd: 51 (zero even), 42 (one even), 60 (one even) 3 digits:
One even, two odd: 321 (zero even), 510 (one even) 4 digits:
One even, three odd: 3210 (one even)
The integers are:
From Case 1: 51 (0 even digits)
From Case 2: 6 (1 even digit), 42 (1 even digit), 60 (1 even digit), 321 (0 even digits), 510 (1 even digit), 3210 (1 even digit)
The positive integers with strictly decreasing digits and at most one even digit, and sum of digits equal to 6 are: 6, 51, 42, 60, 321, 510, 3210.
There are 7 such integers.
Final Answer: The final answer is
7
Question 1210211: How many positive integers are there whose digits strictly decrease from left to right, and have at most one even digit, and the sum of the digits is 6?
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How many positive integers are there whose digits strictly decrease from left to right,
and have at most one even digit, and the sum of the digits is 6?
~~~~~~~~~~~~~~~~~~~~~~~~~
The answer in the post by @CPhill is incorrect.
The numbers satisfying the imposed conditions are
6, 51, 510, 321.
The number of such numbers is 4.
Solved.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the positive integer have digits d
1
d
2
…d
k
such that 9≥d
1
>d
2
>⋯>d
k
≥0 and d
1
+d
2
+⋯+d
k
=6.
The digits are strictly decreasing, so all digits are distinct.
The sum of the digits is 6.
We consider the number of even digits in the set of digits whose sum is 6.
Case 1: Zero even digits (all odd digits)
The possible distinct odd digits are 1, 3, 5.
The subsets of {1, 3, 5} whose sum is 6 are:
\begin{itemize}
\item Size 1: { } (sum is 0, not 6)
\item Size 2: {1, 5} (sum is 6). Integer: 51
\item Size 3: {1, ?, ?} (minimum sum is 1+3+5 = 9 > 6)
\end{itemize}
So, from this case, we have the integer 51.
Case 2: One even digit
The possible distinct even digits are 0, 2, 4, 6, 8.
The possible distinct odd digits are 1, 3, 5, 7, 9.
Subcase 2.1: One even digit
We need a set of distinct digits including exactly one even digit, whose sum is 6.
\begin{itemize}
\item Size 1: {6}. Integer: 6
\item Size 2: {e,o} where e+o=6. Possible pairs (even, odd) with e>o: (4, 2) - not strictly decreasing, (6, 0) - integer 60. Pairs with o>e: (5, 1) - already counted, (3, 3) - not distinct.
\item Size 3: {e,o
1
,o
2
} where e+o
1
+o
2
=6 and o
1
>o
2
. Possible sets: {4,1,?} (sum too small), {2,3,1}. Integer 321. {0,5,1}. Integer 510.
\item Size 4: {e,o
1
,o
2
,o
3
} where e+o
1
+o
2
+o
3
=6. Possible sets: {4,1,?,?}, {2,3,1,0}. Integer 3210.
\end{itemize}
Let's enumerate based on the number of digits:
1 digit: 6 (one even digit)
2 digits:
One even, one odd: 51 (zero even), 42 (one even), 60 (one even) 3 digits:
One even, two odd: 321 (zero even), 510 (one even) 4 digits:
One even, three odd: 3210 (one even)
The integers are:
From Case 1: 51 (0 even digits)
From Case 2: 6 (1 even digit), 42 (1 even digit), 60 (1 even digit), 321 (0 even digits), 510 (1 even digit), 3210 (1 even digit)
The positive integers with strictly decreasing digits and at most one even digit, and sum of digits equal to 6 are: 6, 51, 42, 60, 321, 510, 3210.
There are 7 such integers.
Final Answer: The final answer is
7
Question 1210210: How many positive integers are there whose digits strictly decrease from left to right, and the sum of the digits is 6?
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How many positive integers are there whose digits strictly decrease from left to right,
and the sum of the digits is 6?
~~~~~~~~~~~~~~~~~~~~~~~~~
The answer in the post by @CPhill is incorrect.
The numbers satisfying the imposed conditions are
6, 60, 51, 510, 42, 420, 321, 3210.
The number of such numbers is 8.
Solved.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the positive integer have digits $d_1 d_2 \dots d_k$ such that $9 \ge d_1 > d_2 > \dots > d_k \ge 0$ and $d_1 + d_2 + \dots + d_k = 6$.
Since the digits are strictly decreasing and non-negative, all the digits must be distinct.
Also, since the sum of the digits is 6, the number of digits cannot be too large. The maximum possible number of digits occurs when the digits are $5, 1$, or $4, 2$, or $3, 2, 1$, or $6$.
We consider the possible sets of distinct digits whose sum is 6:
Case 1: One digit
The only possibility is the digit 6. The number is 6. (1 integer)
Case 2: Two digits
We need two distinct digits $d_1 > d_2$ such that $d_1 + d_2 = 6$. The possible pairs are (5, 1) and (4, 2). The corresponding integers are 51 and 42. (2 integers)
Case 3: Three digits
We need three distinct digits $d_1 > d_2 > d_3$ such that $d_1 + d_2 + d_3 = 6$. The only possible set of digits is {3, 2, 1}. The corresponding integer is 321. (1 integer)
Case 4: Four digits
We need four distinct digits $d_1 > d_2 > d_3 > d_4$ such that $d_1 + d_2 + d_3 + d_4 = 6$. The only possible set of digits is {3, 2, 1, 0}. The corresponding integer is 3210. (1 integer)
Case 5: More than four digits
If there are 5 distinct non-negative digits, the minimum sum would be $4 + 3 + 2 + 1 + 0 = 10$, which is greater than 6. So, we cannot have more than 4 digits.
The positive integers satisfying the conditions are 6, 51, 42, 321, and 3210.
The number of such integers is $1 + 2 + 1 + 1 = 5$.
Final Answer: The final answer is $\boxed{5}$
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910, 8911..8955, 8956..9000, 9001..9045, 9046..9090, 9091..9135, 9136..9180, 9181..9225, 9226..9270, 9271..9315, 9316..9360, 9361..9405, 9406..9450, 9451..9495, 9496..9540, 9541..9585, 9586..9630, 9631..9675, 9676..9720, 9721..9765, 9766..9810, 9811..9855, 9856..9900, 9901..9945, 9946..9990, 9991..10035
|



