Question 995681: How many 4-digit numbers greater than 1000 are there that use the four digits of 2012?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If we put some distinguishing marks on the 2's,
we have 4 distinct items:  , ,  , ,  , and , and  . .
The first digit cannot be  , because that would make the number less than 100. , because that would make the number less than 100.
(It would really be a 3-digit number in disguise, too).
So, we have 3 choices for the first digit.
For each of those choices, there will be 3 items left, to chose a 2nd digit from, for a total of  choices for the first two digits. choices for the first two digits.
For each of those  choices, we still have to choose one of the choices, we still have to choose one of the  remaining elements as the third digit, giving us remaining elements as the third digit, giving us  sequences of 4 elements, where we can distinguish sequences of 4 elements, where we can distinguish  from from  . .
However, taking those permutations of elements as numbers,
we would not distinguish between pairs with  from from  in different orders, in different orders,
like 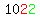 and and 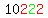 , ,
which both represent number 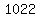 . .
So we need to divide by  , to find that there are , to find that there are
 numbers greater than 1000 that can be made using the four digits of 2012. numbers greater than 1000 that can be made using the four digits of 2012.
|
|
|