Question 995031: Hello,
Let's say I have three letters; A, B and C. I need to know the formula how to count the number of all possible combinations using A, B and C, the letters can be repeated and the order of the letters is important (e.g. ABC and BCA are not the same).
All the way here I'm pretty confident I can solve this alone.  right? right?
Moving on, what if the number of digits can be 1, 2 or 3? (e.g. A, B, C, AA, AB, ..., AAA, AAB, ABC, ... )
Is there a way to count that any faster way than 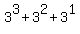 ? ?
It is very time consuming if there can be any more than three digits in the answer and I have to manually solve it as shown above.
Thank you for your time!
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! For A, B, C, the maximum number of combinations is
2*3^0 + 2*3^1 + 2*3^2 + 1 or
2[(3^0)+(3^1)+(3^2)]+1 =
2[1+3+9]+1 = 27
This is not hard to prove if you think of what you have as a base-3 number system counting from the lowest three digit combo to the highest three digit combo.
|
|
|