SOLUTION: How many solutions (using only non-negative integers) are there to the following equation? x1 + x2 + x3 + x4 + x5 = 33

Suppose you have a row of 33+5-1 or 37 o's in a row like this: 

o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o 

Suppose we choose 5-1 or 4 of these to color black, like this:

o o o o o o o ● o o o o ● o o ● o o o o o o o ● o o o o o o o o o o o o o 

There are 7 o's left of the first ●. 
There are 4 o's between the 1st and 2nd ●'s. 
There are 2 o's between the 2nd and 3rd ●'s.
There are 7 o's between the 3rd and 4th ●'s.
There are 13 o's right of the 4th ●.

This represents the solution 7+4+2+7+13 = 33 to x1 + x2 + x3 + x4 + x5 = 33

--------------------------------- 

Suppose we pick these 4 to color black:

o o o o o o o o o o o o o o o o ● ● ● ● o o o o o o o o o o o o o o o o o

There are 16 o's left of the first ●. 
There are 0 o's between the 1st and 2nd ●'s. 
There are 0 o's between the 2nd and 3rd ●'s.
There are 0 o's between the 3rd and 4th ●'s.
There are 17 o's right of the 4th ●.

This represents the solution 16+0+0+0+17 = 33 to x1 + x2 + x3 + x4 + x5 = 33

--------------------------------- 

Or these:

o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o ● ● ● ●

There are 33 o's left of the first ●. 
There are 0 o's between the 1st and 2nd ●'s. 
There are 0 o's between the 2nd and 3rd ●'s.
There are 0 o's between the 3rd and 4th ●'s.
There are 0 o's right of the 4th ●. 

This represents the solution 33+0+0+0+0 = 33 to x1 + x2 + x3 + x4 + x5 = 33

-------------------------------

Or these:

● o o o o o o o o o o o ● o o o o o o o o o o o ● o o o o o o o o o o o ●

There are 0 o's left of the first ●. 
There are 11 o's between the 1st and 2nd ●'s. 
There are 11 o's between the 2nd and 3rd ●'s.
There are 11 o's between the 3rd and 4th ●'s.
There are 0 o's right of the 4th ●. 

This represents the solution 0+11+11+11+0 = 33 to x1 + x2 + x3 + x4 + x5 = 33

-------------------------------

So we see that any solution of x1 + x2 + x3 + x4 + x5 = 33 can be represented
by coloring 4 of the 37 o's black.

So we have 37 o's choose 4 to color black.

Answer:  37C4 = 66045 

The formula for the number of unordered partitions of n into the sum of
r non-negative integers is {n+r-1)C(r-1) or maybe you write it .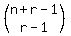  
This is the case n=33 and r=5

Edwin