SOLUTION: Decide if the following scenario involves a permutation or combination. Then find the number of possibilities. There are 50 applicants for two Systems Engineer positions at a l

To determine whether it's a permutation or a combination problem, ask yourself
this question about a sample pair of applicants:

"Does the order they are in matter?"

Which is to ask:

"Is the pair of applicants 

"John Smith and Jane Doe" 

and the pair of applicants

"Jane Doe and John Smith"

the same pair of applicants or a different pair of applicants?

The answer is "They are the same pair of applicants", so the order they are in
does not matter, so this is a combination problem.

20 applicants choose 2 = "20 choose 2" = "20C2" =  = 190

Answer = 190

------------------------

One word of caution here.  If the two positions were totally different, say one
position was for a crane operator and the other for a truck driver, then it
would make a difference if

"John Smith gets the crane operator job and 
Jane Doe gets the truck driver job"

or whether

"Jane Doe gets the crane operator job and 
John Smith gets the truck driver job"

Then we would have a permutations problem.  It would be

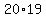20 applicants position 2 = "20C2" =  = 380

But we aren't told that they are different jobs, so we assume they are not,
so the order doesn't matter, and it is a combinations problem.

Edwin