SOLUTION: seven white balls and three black balls are randomly placed in a row. find the probability that no two black balls r placed together.

The 7 white balls can be arranged 7! ways in a row.

For each of those, there are 8 positions to insert the 
3 black balls among the 7 white balls, since no two can 
be together.  They are:

1.  Left of the 1st white ball.
2.  Between the 1st and 2nd white balls.
3.  Between the 2nd and 3rd white balls.
4.  Between the 3rd and 4th white balls.
5.  Between the 4th and 5th white balls.
6.  Between the 5th and 6th white balls.
7.  Between the 6th and 7th white balls.
8.  Right of the 7th white ball.

So we can choose the positions in which to insert the 3 black 
balls in 8C3 ways.

Then for each of those selections of 3 positions to insert the 
3 black balls, there are 3! ways those 3 black balls can be 
arranged in those 3 positions.

So 7!*8C3*3! = 5040*56*6 = 1693440

That's the numerator of the desired probability.

The denominator is the number of ways the 10 balls can be
arranged in a row, or 10! = 3628800

Desired probability =  =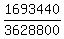 

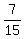Edwin