Question 973681: How many ways can the letter in the word OPTIMISM be rearranged?
What I did:
2 Is, 2 Ms, 1 O, 1 P, 1 T, 1 S = (8,2)(6,2)(4,1)(3,1)(2,1)(1,1)

which I got 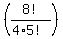
Did I do that correctly?
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website! How many ways can the letter in the word OPTIMISM be rearranged?
What I did:
2 Is, 2 Ms, 1 O, 1 P, 1 T, 1 S = (8,2)(6,2)(4,1)(3,1)(2,1)(1,1)

which I got 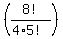
Did I do that correctly?
I'm afraid not.
OPTIMISM is an 8-letter word. If the word were "oPTimISM" the answer would be
8! =40320 because we would be able to tell the difference between the arrangements
mSiToPIM, mSIToPiM, MSIToPIm, MSiToPIm
But since we cannot because the I's and M's look the same, we must divide the
9! by the number of ways the I's can be swapped, which is 2! and also by the
number of ways the M's can be swapped, which is also 2!.
Answer =  = 10080
You see, we had to divide by 2!2! = 4 because, as we saw with the four arrangements
mSiToPIM, mSIToPiM, MSIToPIm, MSiToPIm, all look the same as MSITOPIM
every arrangement is counted 4 times too many in the 8!, that's why we divide
by 4. We divide by the factorial of the number of times each letter is
repeated.
Edwin = 10080
You see, we had to divide by 2!2! = 4 because, as we saw with the four arrangements
mSiToPIM, mSIToPiM, MSIToPIm, MSiToPIm, all look the same as MSITOPIM
every arrangement is counted 4 times too many in the 8!, that's why we divide
by 4. We divide by the factorial of the number of times each letter is
repeated.
Edwin
|
|
|