SOLUTION: A party of 6 is to be formed from 10 men and 7 women so as to include 3 men and 3 women. In how many ways the party can be formed if two particular women refuse to join it?

Then those 2 women are totally out of the picture, so we just ignore them and
rewrite the problem without them, and include only the 5 other women:

We choose the men:

10 men Choose 3 = 10C3 = 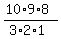 = 120 ways.

For each of those 120 ways to choose the men,

we choose the women:

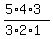5 women Choose 3 = 5C3 =  = 10 ways.

That's (120)(10) = 1200 ways.

[Note: I'm puzzled as to why a problem would bother just to exclude 2 women.
Are you sure that the problem didn't say that they despise each other and that
either one can be invited but not both?  That would change the answer.]

Edwin