A Bag contains 13 red balls numbered 1 - 13 and 5 green balls numbered 14 - 18.
1.) You choose a ball at random. What is the probability that you choose a red OR an even numbered ball?
We will succeed if we choose one of these 16 balls: 1-13,14,16,18.
So the probability is 16 out of the 13+5 or 18 balls. 16 out of 18 is
{{16/18}}} which reduces to 
.
2.) You randomly choose 2 balls from the bag AT THE SAME TIME. What is the
probability that you will choose a red and a green ball?
There are 13 ways to choose a red ball. For each of those 5 ways to choose
the red ball, there are 5 ways to choose the green ball, so there are 13*5
or 65 ways to choose a pair {red,green}.
Now we calculate the number of ways to choose ANY 2 balls:
There are 18C2 = "18 choose 2" = "the combinations of 18 things taken 2 at a
time" = 
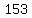So there are 65 ways out of 153 to succeed in getting one of each color.
65 out of 153 is 
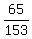Here's a computer generated listing to show this:
That's these 65 ways:
{1,14}, {1,15}, {1,16}, {1,17}, {1,18},
{2,14}, {2,15}, {2,16}, {2,17}, {2,18},
{3,14}, {3,15}, {3,16}, {3,17}, {3,18},
{4,14}, {4,15}, {4,16}, {4,17}, {4,18},
{5,14}, {5,15}, {5,16}, {5,17}, {5,18},
{6,14}, {6,15}, {6,16}, {6,17}, {6,18},
{7,14}, {7,15}, {7,16}, {7,17}, {7,18},
{8,14}, {8,15}, {8,16}, {8,17}, {8,18},
{9,14}, {9,15}, {9,16}, {9,17}, {9,18},
{10,14}, {10,15}, {10,16}, {10,17}, {10,18},
{11,14}, {11,15}, {11,16}, {11,17}, {11,18},
{12,14}, {12,15}, {12,16}, {12,17}, {12,18},
{13,14}, {13,15}, {13,16}, {13,17}, {13,18}
out of these 153 ways:
{1,2}, {1,3}, {1,4}, {1,5}, {1,6}, {1,7}, {1,8}, {1,9}, {1,10}, {1,11}, {1,12}, {1,13}, {1,14}, {1,15}, {1,16}, {1,17}, {1,18},
{2,3}, {2,4}, {2,5}, {2,6}, {2,7}, {2,8}, {2,9}, {2,10}, {2,11}, {2,12}, {2,13}, {2,14}, {2,15}, {2,16}, {2,17}, {2,18},
{3,4}, {3,5}, {3,6}, {3,7}, {3,8}, {3,9}, {3,10}, {3,11}, {3,12}, {3,13}, {3,14}, {3,15}, {3,16}, {3,17}, {3,18},
{4,5}, {4,6}, {4,7}, {4,8}, {4,9}, {4,10}, {4,11}, {4,12}, {4,13}, {4,14}, {4,15}, {4,16}, {4,17}, {4,18},
{5,6}, {5,7}, {5,8}, {5,9}, {5,10}, {5,11}, {5,12}, {5,13}, {5,14}, {5,15}, {5,16}, {5,17}, {5,18},
{6,7}, {6,8}, {6,9}, {6,10}, {6,11}, {6,12}, {6,13}, {6,14}, {6,15}, {6,16}, {6,17}, {6,18},
{7,8}, {7,9}, {7,10}, {7,11}, {7,12}, {7,13}, {7,14}, {7,15}, {7,16}, {7,17}, {7,18},
{8,9}, {8,10}, {8,11}, {8,12}, {8,13}, {8,14}, {8,15}, {8,16}, {8,17}, {8,18},
{9,10}, {9,11}, {9,12}, {9,13}, {9,14}, {9,15}, {9,16}, {9,17}, {9,18},
{10,11}, {10,12}, {10,13}, {10,14}, {10,15}, {10,16}, {10,17}, {10,18},
{11,12}, {11,13}, {11,14}, {11,15}, {11,16}, {11,17}, {11,18},
{12,13}, {12,14}, {12,15}, {12,16}, {12,17}, {12,18},
{13,14}, {13,15}, {13,16}, {13,17}, {13,18},
{14,15}, {14,16}, {14,17}, {14,18},
{15,16}, {15,17}, {15,18},
{16,17}, {16,18},
{17,18}
Edwin
