SOLUTION: In how many ways could 14 people be divided into five groups containing, respectively, 1,2,5,4, and 2 people?

The only difficulty that is presented here is that we have two groups of 2.

First let's do it as though the groups were labeled:

The group of 1 is group A
The first group of 2 is group B
The group of 5 is group C
The group of 4 is group D
The second group of 2 is group E

(14C1)(13C2)(11C5)(6C4)(2C2) = (14)(78)(462)(15)(1) = 7567560

This would be the answer if the groups were labeled.

However, since they are not labeled, this number is twice too many because it
considers, say,

the case where John and Mary are in group B and Sam and Lisa are in group E

as a separate case from

the case where John and Mary are in group E and Sam and Lisa are in group B.

Thus we must divide the 7567560 by 2 to eliminate all such duplications, since
we are not labeling the groups.

Answer: 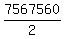 = 3783780

Edwin