Question 969224: 9 people are standing in the queue to the cash-desk (three men, four women and two children). What is the probability that two children and one woman will be standing between some two men?
Answer by Edwin McCravy(20066)   (Show Source): (Show Source):
You can put this solution on YOUR website! 9 people are standing in the queue to the cash-desk (three men, four women and
two children). What is the probability that two children and one woman will be
standing between some two men?
The word "between" is ambiguous. For instance in this number 5837964,
we could say that the 7 is 'between' the 3 and the 9. But using another
way of interpreting "between", we might also say the 7 is 'between' the
8 and the 6, as well as 'between' the 5 and the 6, the 8 and the 4, the
5 and the 4, etc. I will assume you are taking "between" in its most
conservative sense, as "immediately between".
I will therefore assume that to have a "successful" 9-member queue, the
queue must contain a 5-member string of the following 3 types, where
M,W, and C stand for "man", "woman", and "child" respectively:
MWCCM, MCWCM, MCCWM
First we determine the number of such 5-member strings.
We can choose the type of string any of the above 3 ways.
We can then choose the man on the left end any of 3 ways.
We can then choose the man on the right end either of 2 ways.
We can then choose the woman any of 4 ways.
We can then choose the first child either of 2 ways.
We can only choose the second child 1 way.
That's 3*3*2*4*2*1 = 144 ways to choose the 5-member string.
For each of those 144 ways, we have 5 things to arrange,
that is, 4 single people and 1 5-member string. That's 5! ways.
Therefore the total number of "successful" 9-member queues is
144*5! = 144*120 = 17280.
The total number of possible strings is 9! = 362880.
Terefore the desired probability is 17280 successful queues out
of 362880 possible queues, or
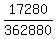 which reduces to which reduces to  .
Edwin .
Edwin
|
|
|