SOLUTION: A multiple choice test has 10 questions. Each question has four answer choices. a. What is the probability a student randomly guesses the answers and gets exactly six question

Algebra ->  Permutations -> SOLUTION: A multiple choice test has 10 questions. Each question has four answer choices. a. What is the probability a student randomly guesses the answers and gets exactly six question      Log On


   

Question 969131: A multiple choice test has 10 questions. Each question has four answer choices.
a. What is the probability a student randomly guesses the answers and gets exactly six questions correct?
b. Is getting exactly 10 questions correct the same probability as getting exactly zero correct? Explain.
c. Describe the steps needed to calculate the probability of getting at least six questions correct if the student randomly guesses. You do not need to calculate this probability!
It would be greatly appreciated if you could show work as to how to solve these, thanks!
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
Binomial probability:

The probability of getting exactly x successes out of n trials, when
the probability of getting 1 success in 1 trial is p is given by the
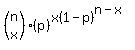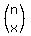formula %28matrix%282%2C1%2Cn%2Cx%29%29%2A%28p%29%5Ex%281-p%29%5E%28n-x%29.

Notice that %28matrix%282%2C1%2Cn%2Cx%29%29 is also written as nCx or C(n,x) or
the number of combinations of n things taken x at a time.

This can also be found with a TI-83 or 84 graphing calculator, press
2ND VARS to find binompdf(n,p,x). Put in numbers for n,p, and x.

A multiple choice test has 10 questions. Each question has four answer choices.
a. What is the probability a student randomly guesses the answers and gets exactly six questions correct?
That's the binomial probability of getting exactly 6 successes in 10 trials with
the probability of 1 success in 1 trial of 1/4.

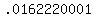
%28matrix%282%2C1%2C10%2C6%29%29%2A%281%2F4%29%5E6%283%2F4%29%5E%2810-6%29%22%22=%22%22.0162220001

b. Is getting exactly 10 questions correct the same probability as getting
exactly zero correct? Explain.
No.  Although both are very unlikely, it is 3 times as likely to guess an answer
incorrectly than to guess it correctly.  So it is more likely to guess them all
incorrectly than all correctly.  (However, in a true-false test, they would be
the same.)

c. Describe the steps needed to calculate the probability of getting at least
six questions correct if the student randomly guesses. You do not need to
calculate this probability!
You would do these steps:

1. Calculate the probability of getting exactly 6 correct.
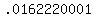%28matrix%282%2C1%2C10%2C6%29%29%2A%281%2F4%29%5E6%283%2F4%29%5E%2810-6%29%22%22=%22%22.0162220001
2. Calculate the probability of getting exactly 7 correct.
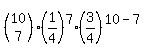
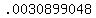%28matrix%282%2C1%2C10%2C7%29%29%2A%281%2F4%29%5E7%283%2F4%29%5E%2810-7%29%22%22=%22%22.0030899048
3. Calculate the probability of getting exactly 8 correct.
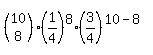
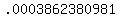%28matrix%282%2C1%2C10%2C8%29%29%2A%281%2F4%29%5E8%283%2F4%29%5E%2810-8%29%22%22=%22%22.0003862380981
4. Calculate the probability of getting exactly 9 correct.
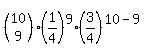
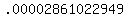%28matrix%282%2C1%2C10%2C9%29%29%2A%281%2F4%29%5E9%283%2F4%29%5E%2810-9%29%22%22=%22%22.00002861022949
5. Calculate the probability of getting all 10 correct.
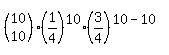
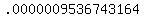%28matrix%282%2C1%2C10%2C10%29%29%2A%281%2F4%29%5E10%283%2F4%29%5E%2810-10%29%22%22=%22%22.0000009536743164

Then you would add them all up and you'd get: .0197277069

Edwin