Question 949746: 7 freshmen, 6 sophomores, 7 juniors, and 4 seniors are eligible to be on a committee.
In how many ways can a dance committee of 18 students be chosen if it is to consist of at least 1 freshmen, 1 sophomore, 2 juniors, 2 seniors, and the rest can be of any grade?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is just my interpretation. Judge for yourself, because I may be overlooking some mistake.
There are lots of ways to make a committee of 18 students,
if you have  eligible candidates. eligible candidates.
In fact there are

possible groups of 18 people that can be selected from a pool 24 people,
or from a different point of view,
there are 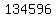 possible groups of 6 rejected candidates that you can send home. possible groups of 6 rejected candidates that you can send home.
However, some of those 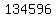 possible committees will fail the requirement to consist of at least 1 freshmen, 1 sophomore, 2 juniors, and 2 seniors. possible committees will fail the requirement to consist of at least 1 freshmen, 1 sophomore, 2 juniors, and 2 seniors.
How many of the 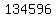 possible committees fail the requirement, and how/why do they fail? possible committees fail the requirement, and how/why do they fail?
No committee can fail because of not including 1 freshman,
because without the 7 freshmen, we have only
 eligible candidates, and that is not enough for an 18-member committee. eligible candidates, and that is not enough for an 18-member committee.
Can a committee of 18 fail to include 1 sophomore?
Yes, because we have  of the of the 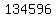 possible committees. possible committees.
We cannot count that a  committee. committee.
Can a committee of 18 fail to include 2 juniors?
Yes, while it is impossible to exclude all 7 juniors,
and form the committee with the  remaining candidates, remaining candidates,
we can send home 6 juniors,
and still have  members for our committee. members for our committee.
We can do that 7 different ways,
keeping a different one of the 7 juniors for the committee.
That way we could make  different committees different committees
that would fail to have the requisite 2 juniors.
We cannot count those  committees, either. committees, either.
Can a committee of 18 fail to include 2 seniors?
Excluding all 4 seniors,
we would still have  students for our committee. students for our committee.
With those 20 students, we could make

different committees that fail the 2-senior requirement,
because they have no senior.
We could also send 3 seniors home,
and have  students left to form an 18-member committee. students left to form an 18-member committee.
that would fail the requirement to have 2 seniors, because it would have only one senior.
We would have 4 choices as to what senior we would keep,
and for each of those choices,
we would still have to pick 17 more students from the 20 non-seniors.
We would have  possible groups of 17 non-seniors, possible groups of 17 non-seniors,
that combined with 4 different choices of one senior would make
 committees with only 1 freshman. committees with only 1 freshman.
So, we have to exclude from the total of 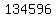 possible committees possible committees
the  committee with no sophomore, committee with no sophomore,
the 7 committees with only 1 junior,
the 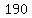 committees with no senior, and committees with no senior, and
the  committees with only 1 freshman. committees with only 1 freshman.
Counting them all, that is  committees that fail the requirement one way or another. committees that fail the requirement one way or another.
Could there be one or more committees counted twice in those 4758, because they fail to meet the requirement more than one way?
The committee that is missing a sophomore includes all the non-sophomores, so it cannot fail by missing any other requirement,
and the committees that have only 1 junior, must include all non-juniors,, so it cannot fail by missing any other requirement.
As for the seniors, a committee with only one, and a committee with none cannot be the same, and I think I am counting them properly.
Subtracting those  committees that fail the requirement, committees that fail the requirement,
we are left with
 committees that meet the requirement. committees that meet the requirement.
NOTE: The folks at the forum in the artofproblemsolving website would probably instantly answer this question, but they may be too succinct with the explanation, or may feel insulted if it is asked in a forum at a level that considers it too easy a problem;
|
|
|