PROBABILITY
There are 11 letters in PROBABILITY.
if it were spelled
PROBAbIliTY, then the answer would be 11!. For spelled
that way it has one of the B's capital and the other b
a small letter (the same for the I and i). Then we could
tell the difference between, say, these 4 arrangements:
iOYIbRAPBTL, iOYIBRAPbTL, IOYibRAPBTL, and IOYiBRAPbTL,
However, since the 2 B's are indistinguishable, as well
as the 2 I's, we cannot tell those 4 arrangements apart.
All 4 look like IOYIBRAPBTL.
So we must divide 11! by 4. That is, we divide 11! by the
factorials of the numbers of times each letter occurs
in the given word.
Since B and I each occur 2 times in PROBABILITY, we divide
by 2! twice, once for B, and once for I, since each occurs
2 times, So we divide by 2! twice which amounts to dividing
by 2!2! =2*2 or 4. That's why we divide by 4. So the
answer is


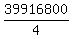

 Edwin
Edwin