SOLUTION: a clerk distributes packages among 4 trucks. what is probability that three packages wind up in different trucks? What is probability if clerk is given 20 packages, that exactly fi

Answer:  

Here's why:

Let the trucks be Truck #1, Truck #2, Truck #3, and Truck #4.

The numerator of the desired probability then is 4. All 3 packages are on one of
the 4 trucks.

Now the denominator is C(6,3) = 20.  Here is why:

Get 3+4 or 7 slips of paper.  (That's 3 packages PLUS 4 trucks

(You don't have to actually get 7 slips of paper.  You can just imagine them,
but I'll talk as though you actually have 7 slips of papers laid out in a row
left to right in front of you). 

Write the word "Truck #4" on the right-most slip of paper.

Now choose 3 other slips of paper from the other 6.  You can choose them
C(6,3) = 20 ways.  

[That's the total number of ways the 3 packages can be placed on the 4 trucks.
I will now explain why].

Write "Truck #1" on the first one you chose, going left to right.  Write "Truck
#2" on the next one you chose, and "Truck #3" on the other one you chose.

So now we have a row of 7 slips of paper. 4 of the slips of paper, including the
very last one, (the rightmost one), have "Truck #1, #2, or #3 written on them.
And 3 slips of paper have nothing written on them.

Now going left to right, count the number of slips of paper that have nothing
written on them which are left of the slip of paper with Truck #1 written on it,
which may be anything from none at all, 0 (zero) through 3. Whatever that number
is, put that number of packages on Truck #1.

Next count the slips of paper between the slips of paper with Truck #1 and Truck
#2, and place that number of packages on Truck #2.  

Next count the slips of paper between the slips that read Truck #2 and Truck #3,
and place that number of packages on Truck #3.  

Finally count the slips of paper between the slips that read Truck #3 and Truck
#4, and place that number of packages on Truck 4.  

Now you can see why the number of ways we can pick the 3 slips of paper to label
with truck numbers (besides the one on the right end labeled Truck #4) is 
6C3 = 20.

So the probability is 4 ways out of 20 or 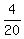 which reduces to 

------------------------------------------------

You can just memorize the formula, the number of ways to put n things into r
groups, including putting 0 in some of the groups is 

(n+r-1)C(r-1)

--------------------

The numerator of the probability is 1, and the denominator is 

(20+4-1)C(4-1) = 23C3 = 1771 

You can also think of this one with 24 slips of paper.  Mark the last one Truck
#4, then pick 3 other slips of paper and label them Trucks #1, #2, and #3. 
Place the same number of packages on each truck as the number of slips of paper
between each pair of successive slips that you chose.

[The number of slips of paper between 2 slips that you picked to write
Truck #n and Truck #(n+1) can be anywhere from 0 to all 20]

Answer: The probability is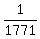 

Edwin