SOLUTION: a committee of four is selected from a group of 20 people. if there are 10 women and 12 men in the group, how many different committees have a majority of men

Algebra ->  Permutations -> SOLUTION: a committee of four is selected from a group of 20 people. if there are 10 women and 12 men in the group, how many different committees have a majority of men       Log On


   

Question 942879: a committee of four is selected from a group of 20 people.
if there are 10 women and 12 men in the group, how many different committees have a majority of men
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
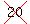a committee of four is selected from a group of cross%2820%2922 people.
if there are 10 women and 12 men in the group, how many different committees
have a majority of men 
Notice that I crossed out the 20 and put 22 so it would make sense.
 10 women and 12 men is 22 people, not only 20 people.

The group of 4, to have a majority of men, would have either

Case 1.  3 men and 1 woman 

or 

Case 2.  4 men.

------------

In case 1 we have 12 men CHOOSE 3, that's 12C3 = 220 ways to choose the 3
men.  For each of those 20 ways, we have 10 women CHOOSE 1, that's 10C1=10.
So, for case 1, there are 220×10 = 2200.

In case 2 we have 12 men CHOOSE 4, that's 12C4 = 495 ways to choose the 4
men. So for case 2, there are 495.

Grand total for both cases = 2200+495 = 2695.

Edwin