Given the word BASKETBALL. How many permutations begin with the letter
K?
This is the same as the number of distinguishable arrangements of
"BASETBALL" (with no "K"), because we can insert a "K" in front of
each distinguishable arrangement of "BASETBALL" and have a
distinguishable arrangement of "BASKETBALL beginning with "K".
"BASETBALL" has 9 letters, with 2 indistinguishable A's, 2
indistinguishable B's, and 2 indistiguishable L's. So there are
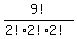 = 45360 distinguishable arrangements of "BASETBALL"
that we can insert a "K" in front of to make a distinguishable
arrangement of "BASKETBALL" which begins with "K".
Answer:
= 45360 distinguishable arrangements of "BASETBALL"
that we can insert a "K" in front of to make a distinguishable
arrangement of "BASKETBALL" which begins with "K".
Answer: 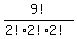 = 45360
= 45360
And How many permutations have the 2 L's together?
This is the same as the number of distinguishable arrangements of
"BASKETBAL" (with just 1 "L"), because we can insert another "L" beside
each "L" in each distinguishable arrangement of "BASKETBAL", and have
a distinguishable arrangement of "BASKETBALL" with 2 "L"'s together.
"BASKETBAL" has 9 letters, with 2 indistinguishable A's and 2
indistinguishable B's. So there are 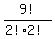 = 90720
distinguishable arrangements of "BASKETBAL" into which we can insert
another L beside each "L" to make a distinguishable arrangement of
"BASKETBALL" with the two "L"'s together.
Answer:
= 90720
distinguishable arrangements of "BASKETBAL" into which we can insert
another L beside each "L" to make a distinguishable arrangement of
"BASKETBALL" with the two "L"'s together.
Answer: 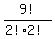 = 90720
Edwin
= 90720
Edwin