SOLUTION: Twenty five points no three of which are collinear are given in the plane. A) How many straight lines do they determine? B) How many triangles do they determine?

Algebra ->  Permutations -> SOLUTION: Twenty five points no three of which are collinear are given in the plane. A) How many straight lines do they determine? B) How many triangles do they determine?      Log On


   

Question 934543: Twenty five points no three of which are collinear are given in the plane.
A) How many straight lines do they determine?
B) How many triangles do they determine?
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
Suppose the points are labeled with the letters A,B,C,...,Y

(A) A straight line is determined by two points.  There are C(25,2) choices of
pairs of those 25 letters.  That's 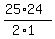%2825%2A24%29%2F%282%2A1%29 = 300 straight lines.

(B) A triangle is determined by three points which are not collinear.  There are
C(25,3) choices of groups of 3 of those 25 letters.  That's 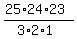%2825%2A24%2A23%29%2F%283%2A2%2A1%29 = 2300 triangles.

Edwin