Question 909251: a group of 630 children is seated in row for a group photo session. each row contains three less children than the row in front of it which one of the following number of row is not possible??
a 2
b 3
c 5
d 6
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website! Your problem states that there is only one correct answer listed,
but there are two correct answers.
--------------------------------------
We'll try them all:
The formula for the sum of an arithmetic series is
  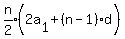
where n = the number of terms and a1 = the first term.
We will set Sn = 630 and d=3 in every case.
n will be the number of rows and a1 will be the number
of children in the first, shortest, row.
--------------------------------------
We try n = 2
  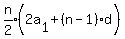
  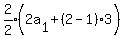
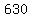  
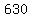  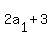
  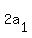
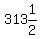  
That would be 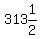 children in one row and children in one row and
3 less or 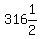 is the second row. is the second row.
That would add up to 630 children, but it's not nice to
cut children in half, :) so you can't have 2 rows.
That's one answer.
--------------------------------------
We try n = 3
  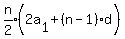
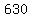  
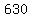  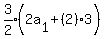
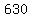  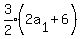
Multiply both sides by 2 to clear the fraction
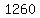  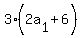
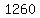  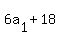
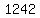  
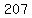  
You have 3 rows with 207, 210, and 213
and 207+210+213 = 630. That's possible so it isn't a
correct answer
--------------------------------------
We try n = 5
  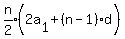
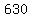  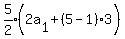
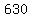  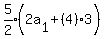
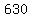  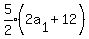
Multiply both sides by 2 to clear the fraction
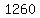  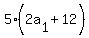
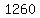  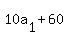
  
  
You have 4 rows with 120, 123, 126, 129 and 132
and 120+123+126+129 = 630. That's possible so it isn't a
correct answer.
--------------------------------------
We try n = 6
  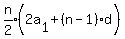
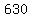  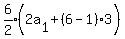
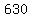  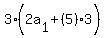
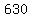  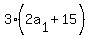
Divide both sides by 3
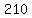  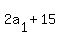
  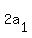
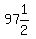  
You have 6 rows of 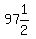 , ,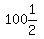 , ,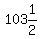 , ,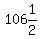 , ,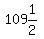 , ,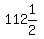 . That adds to 630, but we'd have to cut . That adds to 630, but we'd have to cut
3 children in half. So that's not a possibility either. So 6 is a
correct answer also.
So two of the choices are correct, 2 and 6.
Edwin
|
|
|