I'll assume that MISSISSIPPI was mispelled. It has 4 S's and 2 P's.
If you meant "MISSISIPI", there are so few you can just list them all
easier than calculating them, for it's just the 6 permutations of
M,P,(SSS) with 4 I's separating them:
IMIPISSSI
IMISSSIPI
IPIMISSSI
IPISSSIMI
ISSSIMIPI
ISSSIPIMI
Assuming you meant the correct spelling of the state:
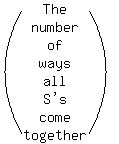

 The number of ways the four S's can come together
The letters of MISSISSIPPI arranged in alphabetical order is
I,I,I,I,M,P,P,S,S,S,S
The number of ways the four S's can come together is the number of
distinguishable permutations of these 8 things, where the (SSSS) is
considered as a single "thing".
I,I,I,I,M,P,P,(SSSS)
Since there are 4 indistinguishable I's and 2 indistinguishable P's,
the number is:
The number of ways the four S's can come together
The letters of MISSISSIPPI arranged in alphabetical order is
I,I,I,I,M,P,P,S,S,S,S
The number of ways the four S's can come together is the number of
distinguishable permutations of these 8 things, where the (SSSS) is
considered as a single "thing".
I,I,I,I,M,P,P,(SSSS)
Since there are 4 indistinguishable I's and 2 indistinguishable P's,
the number is:
 From this 840 we must subtract the number of ways 2 or more I's
can come together.
First we will calculate the number of distinguishable arrangements of
M,P,P,(SSSS) with no I's, and then we'll calculate how many ways we
can insert the 4 I's with 2 or more together. Then we'll multiply
those two numbers together.
Again in the distinguishable arrangements of M,P,P,(SSSS), the
(SSSS) is considered as just one thing.
Since there are 2 indistinguishable P's, the number is:
From this 840 we must subtract the number of ways 2 or more I's
can come together.
First we will calculate the number of distinguishable arrangements of
M,P,P,(SSSS) with no I's, and then we'll calculate how many ways we
can insert the 4 I's with 2 or more together. Then we'll multiply
those two numbers together.
Again in the distinguishable arrangements of M,P,P,(SSSS), the
(SSSS) is considered as just one thing.
Since there are 2 indistinguishable P's, the number is:
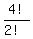 = 12
An example would be PMP(SSSS). Let's put a space before and after
each letter or "thing" to indicate feasible places to insert the I's.
_P_M_P_(SSSS)_
So there are 5 places to insert the four I's.
Case 1. All four I's come together (IIII).
That's 5 ways.
Case 2. The I's are split 3 and 1, (III) and (I).
Place the (III) any of 5 ways
Place the (I) in any of the 4 remaining places
That's 5*4 or 20 ways.
Case 3. The I's are split 2 and 2. (II) and (II)
Choose the 2 places for them to go in C(5,2) or 10 ways
That's 10 ways.
Case 4. The I's are split 2,1 and 1. (II),(I), and (I)
Choose the places for the two single (I)'s C(5,2) = 10 ways
Choose the place for the (II) as any of the remaining 3 ways
That's 10*3 or 30 ways.
For those four cases that's 5+20+10+30 = 65 ways.
We multiply this 65 by the 12 distinguishable arrangements of M,P,P,(SSSS),
That's 65*12 or 780 ways.
That's the number which we must subtract from the 840.
Final answer = 840 - 780 = 60 distinguishable permutations.
Here they all are, computer generated, 10 rows of 6 each:
IMIPIPISSSS IMIPIPSSSSI IMIPISSSSIP IMIPISSSSPI IMIPPISSSSI IMIPSSSSIPI
IMISSSSIPIP IMISSSSIPPI IMISSSSPIPI IMPIPISSSSI IMPISSSSIPI IMSSSSIPIPI
IPIMIPISSSS IPIMIPSSSSI IPIMISSSSIP IPIMISSSSPI IPIMPISSSSI IPIMSSSSIPI
IPIPIMISSSS IPIPIMSSSSI IPIPISSSSIM IPIPISSSSMI IPIPMISSSSI IPIPSSSSIMI
IPISSSSIMIP IPISSSSIMPI IPISSSSIPIM IPISSSSIPMI IPISSSSMIPI IPISSSSPIMI
IPMIPISSSSI IPMISSSSIPI IPPIMISSSSI IPPISSSSIMI IPSSSSIMIPI IPSSSSIPIMI
ISSSSIMIPIP ISSSSIMIPPI ISSSSIMPIPI ISSSSIPIMIP ISSSSIPIMPI ISSSSIPIPIM
ISSSSIPIPMI ISSSSIPMIPI ISSSSIPPIMI ISSSSMIPIPI ISSSSPIMIPI ISSSSPIPIMI
MIPIPISSSSI MIPISSSSIPI MISSSSIPIPI PIMIPISSSSI PIMISSSSIPI PIPIMISSSSI
PIPISSSSIMI PISSSSIMIPI PISSSSIPIMI SSSSIMIPIPI SSSSIPIMIPI SSSSIPIPIMI
Edwin
= 12
An example would be PMP(SSSS). Let's put a space before and after
each letter or "thing" to indicate feasible places to insert the I's.
_P_M_P_(SSSS)_
So there are 5 places to insert the four I's.
Case 1. All four I's come together (IIII).
That's 5 ways.
Case 2. The I's are split 3 and 1, (III) and (I).
Place the (III) any of 5 ways
Place the (I) in any of the 4 remaining places
That's 5*4 or 20 ways.
Case 3. The I's are split 2 and 2. (II) and (II)
Choose the 2 places for them to go in C(5,2) or 10 ways
That's 10 ways.
Case 4. The I's are split 2,1 and 1. (II),(I), and (I)
Choose the places for the two single (I)'s C(5,2) = 10 ways
Choose the place for the (II) as any of the remaining 3 ways
That's 10*3 or 30 ways.
For those four cases that's 5+20+10+30 = 65 ways.
We multiply this 65 by the 12 distinguishable arrangements of M,P,P,(SSSS),
That's 65*12 or 780 ways.
That's the number which we must subtract from the 840.
Final answer = 840 - 780 = 60 distinguishable permutations.
Here they all are, computer generated, 10 rows of 6 each:
IMIPIPISSSS IMIPIPSSSSI IMIPISSSSIP IMIPISSSSPI IMIPPISSSSI IMIPSSSSIPI
IMISSSSIPIP IMISSSSIPPI IMISSSSPIPI IMPIPISSSSI IMPISSSSIPI IMSSSSIPIPI
IPIMIPISSSS IPIMIPSSSSI IPIMISSSSIP IPIMISSSSPI IPIMPISSSSI IPIMSSSSIPI
IPIPIMISSSS IPIPIMSSSSI IPIPISSSSIM IPIPISSSSMI IPIPMISSSSI IPIPSSSSIMI
IPISSSSIMIP IPISSSSIMPI IPISSSSIPIM IPISSSSIPMI IPISSSSMIPI IPISSSSPIMI
IPMIPISSSSI IPMISSSSIPI IPPIMISSSSI IPPISSSSIMI IPSSSSIMIPI IPSSSSIPIMI
ISSSSIMIPIP ISSSSIMIPPI ISSSSIMPIPI ISSSSIPIMIP ISSSSIPIMPI ISSSSIPIPIM
ISSSSIPIPMI ISSSSIPMIPI ISSSSIPPIMI ISSSSMIPIPI ISSSSPIMIPI ISSSSPIPIMI
MIPIPISSSSI MIPISSSSIPI MISSSSIPIPI PIMIPISSSSI PIMISSSSIPI PIPIMISSSSI
PIPISSSSIMI PISSSSIMIPI PISSSSIPIMI SSSSIMIPIPI SSSSIPIMIPI SSSSIPIPIMI
Edwin