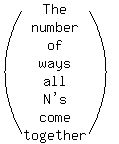
The number of ways the N's can come together
The letters of ENGINEERING arranged in alphabetical order is
E,E,E,G,G,I,I,N,N,N,R
The number of ways the three N's can come together is the number of
distinguishable permutations of these 9 things, where the (NNN) is
considered as a single "thing".
E,E,E,G,G,I,I,(NNN),R
Since there are 3 indistinguishable E's, 2 indistinguishable G's,
and 2 indistinguishable I's, the number is:
From this 15120 we must subtract the number of ways 2 or 3 E's
can come together.
First we will calculate the number of distinguishable arrangements of
these 7 things:
(EE),G,G,I,I,(NNN),R where one E is missing, and then we'll calculate
how many ways we can insert the third E into each one of those. Here
the (EE) and the (NNN) are each considered as just one "thing".
Since there are 2 indistinguishable G's, and 2 indistinguishable I's,
the number is:
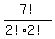= 1260
An example would be GG(EE)II(NNN)R. Let's put a space before and after
each letter or "thing" to indicate feasible places to insert the third
E. We'll number the spaces below each space, like this:
_G_G_(EE)_I_R_(NNN)_I_
1 2 3 4 5 6 7 8
We might think at first that we could insert the 3rd E into any of the
8 spaces. However we would not be able to distinguish between placing
the third E in positions 3 or 4 above. That is, we could not tell the
difference between the result of inserting the third E just before, or
just after, the (EE). So there are 1 less than 8, or only 7 places that
we can insert the third E and have a distinguishable permutation.
So we multiply 1260 by the 7 ways to insert the third E. So 1260×7 =
8820. That is the number which we must subtract from the 15120.
Final answer = 15120 - 8820 = 6300 distinguishable permutations.
Edwin
