SOLUTION: 1How many different ways may a row of on-off switches be set if no two adjacent switches may be off. 2 How many numbers can be made from the digits 2,3,4,5,6 if they are to be g

Let 1 represent a switch that is on
Let 0 represent a switch that is off

A row of 1 switch can be set these and only these 2 ways:

1.  0
2.  1  

A row of 2 switches can be set these and only these 3 ways

1.  01
2.  10
3.  11

A row of 3 switches can be set these and only these 5 ways

1.  010
2.  011
3.  101
4.  110
5.  111

A row of 4 switches can be set these and only these 8 ways

1.  0101
2.  0110
3.  0111
4.  1010
5.  1011
6.  1101
7.  1110
8.  1111

Notice that this list of 4-switch settings consists 
of the 2-switch settings with a "10 annexed at the end

1.  0110
2.  1010
3.  1110  

plus

the 3-switch setting with a 1 annexed at the end

1.  0101
2.  0111
3.  1011
4.  1101
5.  1111 

This suggests the recursion formula:

  

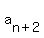This is the Fibonacci recursion formula. 

If the Fibonacci numbers are considered as subscripted this way:

, , , , , ,, etc.

then if there are n switches, there are Fn+2 switch settings 
which have no two adjacent switches which are off.

This is easy compared to (a).

Case 1:  Four digit numbers:

Choose the first digit as any of these 3 digits: {4,5,6}.
Choose the second digit as any of the remaining 4 digits.
Choose the third digit as any of the remaining 3 digits.
Choose the fourth digit as either of the remaining 2 digits.

That's 3*4*3*2 = 72 ways

Case 2:  Five digit numbers:

Same as the four digit number.  Just tack the remaining 1 digit on
the right end of each of the 72 four digit numbers.

That's also 72 ways.

Anwer: 72+72 = 144 ways

Edwin