SOLUTION: The crew of an 8 member rowing team is to be chosen from 12 men , of which 3 can on one side only and 2 can on other side only.find number of ways of arranging the crew with 4 m

Algebra ->  Permutations -> SOLUTION: The crew of an 8 member rowing team is to be chosen from 12 men , of which 3 can on one side only and 2 can on other side only.find number of ways of arranging the crew with 4 m      Log On


   

Question 885176: The crew of an 8 member rowing team is to be chosen from 12 men , of which 3 can
on one side only and 2 can on other side only.find number of ways of arranging the
crew with 4 memembers on each side.
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
Let's divide the 12 up into 3 Ls, 2 R's and 7 E's
The 3 L's can only row on the Left.
The 2 R's can only row on the Right.
The 7 E's can row on Either side.

There are 11 cases to consider

Case 1. 1R, 7E's  

Choose the 1R C(2,1) ways
Seat the 1R P(4,1) ways
Choose and seat the 7E's P(12,7) ways.
Total for case 1: 
C(2,1)P(4,1)P(12,7) = 
2×4×P(12,7) = 8P(12,7)

Case 2. 2R's, 6E's

Choose the 2R's C(2,2)=1 way, 
Seat the 2R's P(4,2) ways.
Choose and seat the 6E's P(12,6) ways.
Total for case 2: 
C(2,2)P(4,2)P(12,6) =
1×12×P(12,6) = 12P(12,6)

Case 3. 1L, 7E's

Choose the 1L C(3,1) ways, 
Seat the 1L P(4,1) ways
Choose and seat the 7E's P(12,7) ways.
Total for case 3: 
C(3,1)C(4,1)P(12,7) =
3×4×P(12,7) = 12P(12,7)


Case 4: 1L, 1R, 6E's
Choose the 1L C(3,1) ways, 
Seat the 1L P(4,1) ways,
Choose the 1R C(2,1) ways, 
Seat the 1R C(4,1) ways,
Choose and seat the 6E's P(12,6) ways.
Total for case 4: 
C(3,1)C(4,1)C(2,1)C(4,1)P(12,6)=
3×4×2×4×P(12,6) = 96P(12,6)

Case 5: 1L, 2R's, 5E's
Choose the 1L C(3,1) ways, 
Seat the 1L P(4,1) ways,
Choose the 2R's C(2,2)=1 way, 
Seat the 2R's P(4,2) ways,
Choose and seat the 5E's P(12,5) ways.
Total for case 5: 
C(3,1)P(4,1)C(2,2)P(4,2)P(12,5) =
3×4×1×12×P(12,5) = 144P(12,5)

Case 6: 2L's, 6E's
Choose the 2L's C(3,2) ways, 
Seat the 2L's P(4,2) ways,
Choose and seat the 6E's P(12,6) ways.
Total for case 6: 
C(3,2)P(4,2)P(12,6)=
3×12×P(12,6) = 36P(12,6)

Case 7: 2L's, 1R, 5E's
Choose the 2L's C(3,2) ways, 
Seat the 2L's P(4,2) ways,
Choose the 1R C(2,1) ways, 
Seat the 1R P(4,1) ways
Choose and seat the 5E's P(12,5) ways.
Total for case 7:
C(3,2)P(4,2)C(2,1)P(4,1)P(12,5) =
3×12×2×4×P(12,5) = 288P(12,5)

Case 8: 2L's, 2R's, 4E's
Choose the 2L's C(3,2) ways, 
Seat the 2L's P(4,2) ways,
Choose the 2R's C(2,2)=1 way, 
Seat the 2R's P(4,2) ways
Choose and seat the 4E's P(12,4) ways.
Total for case 8:
C(3,2)P(4,2)C(2,2)P(4,2)P(12,4)
3×12×1×12×P(12,4) = 432P(12,4).
  
Case 9: 3L's, 5E's
Choose the 3L's C(3,3)=1 way, 
Seat the 3L's P(4,3) ways,
Choose and seat the 5E's P(12,5) ways.
Total for case 6: 
C(3,3)P(4,3)P(12,5)
1×24×P(12,5) = 24P(12,5)

Case 10: 3L's, 1R, 4E's
Choose the 3L's C(3,3)=1 way, 
Seat the 3L's P(4,3) ways,
Choose the 1R C(2,1) ways,
Seat the 1R P(4,1) ways,
Choose and seat the 4E's P(12,4) ways.
Total for case 10: 
C(3,3)P(4,3)C(2,1)P(4,1)P(12,4)
1×24×2×4×P12,4) = 192P(12,4)

Case 11: 3L's, 2R's, 3E's
Choose the 3L's C(3,3)=1 way, 
Seat the 3L's P(4,3) ways,
Choose the R's C(2,2)=1 way,
Seat the 2R's P(4,2) ways,
Choose and seat the 3E's P(12,3) ways.
Total for case 10: 
C(3,3)P(4,3)C(2,2)P(4,2)P(12,3)
1×24×1×12×P(12,3) = 288P(12,3)


Total =

8P(12,7)+12P(12,6)+12P(12,7)+96P(12,6)+

144P(12,5)+36P(12,6)+288P(12,5)+432P(12,4)+

24P(12,5)+192P(12,4)+288P(12,3) = 

(8+12)P(12,7)+(12+96+36)P(12,6)+

(144+288+24)P(12,5)+(432+192)P(12,4)+

288P(12,3) =

20P(12,7)+144P(12,6)+456P(12,5)+624P(12,4)+288P(12,3) =



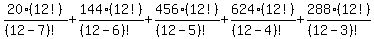Answer =  226765440

Edwin